题目内容
19.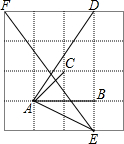 如图是由16个边长为1的小正方形拼成的,任意连接这些小正方形的若干个顶点,可得到一些线段,试分别找出两条长度是有理数的线段和三条长度不是有理数的线段,你能估计出来吗?(结果保留2个有效数字)
如图是由16个边长为1的小正方形拼成的,任意连接这些小正方形的若干个顶点,可得到一些线段,试分别找出两条长度是有理数的线段和三条长度不是有理数的线段,你能估计出来吗?(结果保留2个有效数字)
分析 由图形,利用勾股定理求出AB,AC,AE,AD,以及EF的长即可.
解答 解:根据题意得:
AB=2,AC=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$≈1.4,AE=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$≈2.2,AD=$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$≈3.6,EF=$\sqrt{{3}^{2}+{4}^{2}}$=5.
点评 此题考查了勾股定理,以及实数,熟练掌握勾股定理是解本题的关键.

练习册系列答案
相关题目
10. 如图,直线AC∥BD,AB平分∠CAD,∠1=62°,则∠2的度数是( )
如图,直线AC∥BD,AB平分∠CAD,∠1=62°,则∠2的度数是( )
 如图,直线AC∥BD,AB平分∠CAD,∠1=62°,则∠2的度数是( )
如图,直线AC∥BD,AB平分∠CAD,∠1=62°,则∠2的度数是( )| A. | 50° | B. | 59° | C. | 60° | D. | 62° |
14.在△ABC中,AB=2,AC=3,$\overrightarrow{AB}$•$\overrightarrow{BC}$=1,则BC=( )
| A. | $\sqrt{3}$ | B. | $\sqrt{7}$ | C. | 2$\sqrt{2}$ | D. | $\sqrt{23}$ |
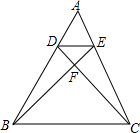 如图,在△ABC中,D、E分别是AB、AC上的点,DC交BE于F,且AD:AB=1:3,AE=$\frac{1}{2}$EC,求证:
如图,在△ABC中,D、E分别是AB、AC上的点,DC交BE于F,且AD:AB=1:3,AE=$\frac{1}{2}$EC,求证: 如图,已知∠ADC=∠ACD,求证:∠α=∠β+2∠γ.
如图,已知∠ADC=∠ACD,求证:∠α=∠β+2∠γ.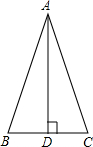 如图,AD是△ABC的高,若AB+BD=AC+CD,求证:△ABC是等腰三角形.
如图,AD是△ABC的高,若AB+BD=AC+CD,求证:△ABC是等腰三角形.