题目内容
7.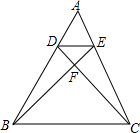 如图,在△ABC中,D、E分别是AB、AC上的点,DC交BE于F,且AD:AB=1:3,AE=$\frac{1}{2}$EC,求证:
如图,在△ABC中,D、E分别是AB、AC上的点,DC交BE于F,且AD:AB=1:3,AE=$\frac{1}{2}$EC,求证:(1)△ADE∽△ABC;
(2)DF•BF=EF•CF.
分析 (1)利用“两边及夹角”法进行证明;
(2)根据(1)可得DE∥BC,由“平行线分线段成比例”进行证明即可.
解答 证明:(1)∵AE=$\frac{1}{2}$EC,
∴AE=$\frac{1}{3}$AC.
又∵AD:AB=1:3,
∴$\frac{AD}{AB}$=$\frac{AE}{AC}$=$\frac{1}{3}$.
又∠DAE=∠BAC,
∴△ADE∽△ABC;
(2)由(1)知,$\frac{AD}{AB}$=$\frac{AE}{AC}$,
∴DE∥BC,
∴$\frac{DF}{CF}$=$\frac{EF}{BF}$,
∴DF•BF=EF•CF.
点评 本题考查了相似三角形的判定与性质.在证明第(2)题时,也可以利用“平行线法“推知△DEF∽△CBF,由该相似三角形的对应边成比例证得结论.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
18.下列各式中,正确的是( )
| A. | -|-5|>0 | B. | -$\frac{4}{7}$>-$\frac{5}{7}$ | C. | |-0.4|<|+0.4| | D. | |-$\frac{1}{2}$|<0 |
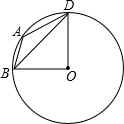 如图,⊙O是△ABD的外接圆,若∠A=135°,则∠BDO=90度.
如图,⊙O是△ABD的外接圆,若∠A=135°,则∠BDO=90度.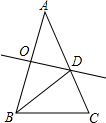 如图,在△ABC中,∠A=36°,AB=AC,AB的垂直平分线OD交AB于O,交AC于D,连接BD.下列结论:①∠C=2∠A;②BD平分∠ABC;③S△BCD=S△BOD;④BC=BD,其中正确的结论有①②④.(只需填序号)
如图,在△ABC中,∠A=36°,AB=AC,AB的垂直平分线OD交AB于O,交AC于D,连接BD.下列结论:①∠C=2∠A;②BD平分∠ABC;③S△BCD=S△BOD;④BC=BD,其中正确的结论有①②④.(只需填序号)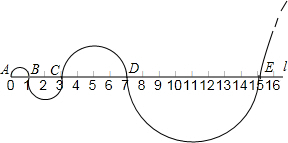 如图,在你标有刻度的直线l上,从点A开始,以AB=1为直径画半圆,记为第1个半圆;以BC=2为直径画半圆,记为第2个半圆;以CD=4为直径画半圆,记为第3个半圆;以DE=8为直径画半圆,记为第4个半圆…,按此规律,则第4个半圆的面积是第3个半圆面积的4倍,第n个半圆的面积为22n-5π.(结果保留π)
如图,在你标有刻度的直线l上,从点A开始,以AB=1为直径画半圆,记为第1个半圆;以BC=2为直径画半圆,记为第2个半圆;以CD=4为直径画半圆,记为第3个半圆;以DE=8为直径画半圆,记为第4个半圆…,按此规律,则第4个半圆的面积是第3个半圆面积的4倍,第n个半圆的面积为22n-5π.(结果保留π)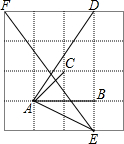 如图是由16个边长为1的小正方形拼成的,任意连接这些小正方形的若干个顶点,可得到一些线段,试分别找出两条长度是有理数的线段和三条长度不是有理数的线段,你能估计出来吗?(结果保留2个有效数字)
如图是由16个边长为1的小正方形拼成的,任意连接这些小正方形的若干个顶点,可得到一些线段,试分别找出两条长度是有理数的线段和三条长度不是有理数的线段,你能估计出来吗?(结果保留2个有效数字) 已知二次函数y=-$\frac{1}{2}$(x+4)2,将此函数的图象向右平移3个单位长度,再向上平移2个单位长度.
已知二次函数y=-$\frac{1}{2}$(x+4)2,将此函数的图象向右平移3个单位长度,再向上平移2个单位长度.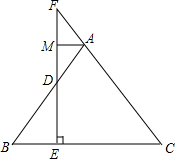 如图所示,在△ABC中,AB=AC,EF⊥BC于点E,点M是DF的中点,试说明AM⊥FD的理由.
如图所示,在△ABC中,AB=AC,EF⊥BC于点E,点M是DF的中点,试说明AM⊥FD的理由.