题目内容
4. 如图,已知∠ADC=∠ACD,求证:∠α=∠β+2∠γ.
如图,已知∠ADC=∠ACD,求证:∠α=∠β+2∠γ.
分析 首先由三角形内角和定理可得∠α+∠β=2∠ACD,由外角的性质可得:∠ADC=∠β+∠γ,等量代换得出结论.
解答 解:在△ADC中,
∵∠ADC=∠ACD,
∴∠CAD=180°-2∠ADC,
∵∠CAD=180°-(∠α+∠β),
∴∠α+∠β=2∠ADC,
∴∠α=2∠ADC-∠β
=2(∠β+∠γ)-∠β
=∠β+2∠γ.
点评 本题主要考查了三角形的内角和定理和外角的性质,综合运用三角形内角和定理和外角的性质是解答此题的关键.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
13.方程x2-2|x|+1=0的不同实数根的个数为( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 小明用图中所示的扇形纸片作一个圆锥侧面,已知扇形的半径为5cm,弧长是6πcm,那么这个圆锥的高是4cm.
小明用图中所示的扇形纸片作一个圆锥侧面,已知扇形的半径为5cm,弧长是6πcm,那么这个圆锥的高是4cm.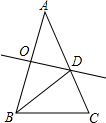 如图,在△ABC中,∠A=36°,AB=AC,AB的垂直平分线OD交AB于O,交AC于D,连接BD.下列结论:①∠C=2∠A;②BD平分∠ABC;③S△BCD=S△BOD;④BC=BD,其中正确的结论有①②④.(只需填序号)
如图,在△ABC中,∠A=36°,AB=AC,AB的垂直平分线OD交AB于O,交AC于D,连接BD.下列结论:①∠C=2∠A;②BD平分∠ABC;③S△BCD=S△BOD;④BC=BD,其中正确的结论有①②④.(只需填序号)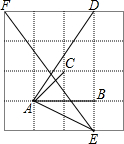 如图是由16个边长为1的小正方形拼成的,任意连接这些小正方形的若干个顶点,可得到一些线段,试分别找出两条长度是有理数的线段和三条长度不是有理数的线段,你能估计出来吗?(结果保留2个有效数字)
如图是由16个边长为1的小正方形拼成的,任意连接这些小正方形的若干个顶点,可得到一些线段,试分别找出两条长度是有理数的线段和三条长度不是有理数的线段,你能估计出来吗?(结果保留2个有效数字)
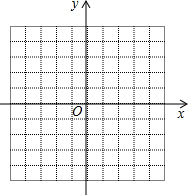 已知二次函数y=-$\frac{1}{2}$(x+4)2,将此函数的图象向右平移3个单位长度,再向上平移2个单位长度.
已知二次函数y=-$\frac{1}{2}$(x+4)2,将此函数的图象向右平移3个单位长度,再向上平移2个单位长度. 如图,直线y=kx+b过点C(1,3)与坐标轴分别交于点A(0,2)和点B.
如图,直线y=kx+b过点C(1,3)与坐标轴分别交于点A(0,2)和点B.