题目内容
3.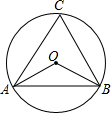 如图,△ABC内接于⊙O,若∠AOB=110°,则∠ACB的度数是( )
如图,△ABC内接于⊙O,若∠AOB=110°,则∠ACB的度数是( )| A. | 70° | B. | 60° | C. | 55° | D. | 50° |
分析 直接根据圆周角定理即可得出结论.
解答 解:∵∠ACB与∠AOB是同弧所对的圆周角与圆心角,∠AOB=110°,
∴∠ACB=$\frac{1}{2}$∠AOB=55°.
故选C.
点评 本题考查的是三角形的外接圆与外心,熟知圆周角定理是解答此题的关键.

练习册系列答案
相关题目
13.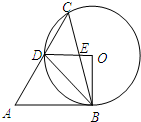 如图,在锐角△ABC中,∠A=60°,∠ACB=45°,以BC为弦作⊙O,交AC于点D,OD与BC交于点E,若AB与⊙O相切,则下列结论错误的是( )
如图,在锐角△ABC中,∠A=60°,∠ACB=45°,以BC为弦作⊙O,交AC于点D,OD与BC交于点E,若AB与⊙O相切,则下列结论错误的是( )
 如图,在锐角△ABC中,∠A=60°,∠ACB=45°,以BC为弦作⊙O,交AC于点D,OD与BC交于点E,若AB与⊙O相切,则下列结论错误的是( )
如图,在锐角△ABC中,∠A=60°,∠ACB=45°,以BC为弦作⊙O,交AC于点D,OD与BC交于点E,若AB与⊙O相切,则下列结论错误的是( )| A. | ∠BOD=90° | B. | DO∥AB | C. | CD=AD | D. | △BDE∽△BCD |
8.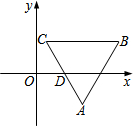 如图,在平面直角坐标系中,△ABC是等边三角形,BC∥x轴,AB=4,AC的中点D在x轴上,且D($\sqrt{3}$,0),则点A的坐标为( )
如图,在平面直角坐标系中,△ABC是等边三角形,BC∥x轴,AB=4,AC的中点D在x轴上,且D($\sqrt{3}$,0),则点A的坐标为( )
 如图,在平面直角坐标系中,△ABC是等边三角形,BC∥x轴,AB=4,AC的中点D在x轴上,且D($\sqrt{3}$,0),则点A的坐标为( )
如图,在平面直角坐标系中,△ABC是等边三角形,BC∥x轴,AB=4,AC的中点D在x轴上,且D($\sqrt{3}$,0),则点A的坐标为( )| A. | (2$\sqrt{3}$,-$\sqrt{3}$) | B. | ($\sqrt{3}$-1,$\sqrt{3}$) | C. | ($\sqrt{3}$+1,-$\sqrt{3}$) | D. | ($\sqrt{3}$-1,-$\sqrt{3}$) |
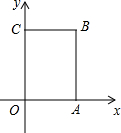 如图,在长方形OABC中,O为平面直角坐标系的原点,点A坐标为(a,0),点C的坐标为(0,b),且a、b满足$\sqrt{a-4}$+|b-6|=0,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O-C-B-A-O的线路移动.
如图,在长方形OABC中,O为平面直角坐标系的原点,点A坐标为(a,0),点C的坐标为(0,b),且a、b满足$\sqrt{a-4}$+|b-6|=0,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O-C-B-A-O的线路移动. 如图,二次函数y=-x2+bx+c的图象(抛物线)与x轴交于A(1,0),且当x=0和x=-2时所对应的函数值相等.
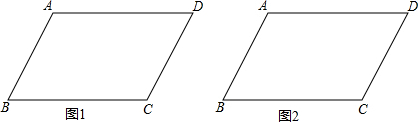
如图,二次函数y=-x2+bx+c的图象(抛物线)与x轴交于A(1,0),且当x=0和x=-2时所对应的函数值相等.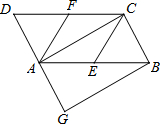 如图,在?ABCD中,E、F分别是边AB、CD的中点,BG∥AC交DA的延长线于点G.
如图,在?ABCD中,E、F分别是边AB、CD的中点,BG∥AC交DA的延长线于点G.