题目内容
18. 如图,已知A,B是反比例函数y=$\frac{k}{x}$(k>0,x>0)图象上的两点,BC∥x轴,交y轴于点C,动点P从坐标原点O出发,先沿射线OA的方向运动到点A,再从点A沿曲线AB运动到点B,最后沿射线BC方向运动到点C,整个运动过程中点P的运动速度保持不变,过点P作PM⊥x轴,PN⊥y轴,垂足分别为M,N,设四边形OMPN的面积为S,点P运动的时间为t,则S关于t的函数图象大致为( )
如图,已知A,B是反比例函数y=$\frac{k}{x}$(k>0,x>0)图象上的两点,BC∥x轴,交y轴于点C,动点P从坐标原点O出发,先沿射线OA的方向运动到点A,再从点A沿曲线AB运动到点B,最后沿射线BC方向运动到点C,整个运动过程中点P的运动速度保持不变,过点P作PM⊥x轴,PN⊥y轴,垂足分别为M,N,设四边形OMPN的面积为S,点P运动的时间为t,则S关于t的函数图象大致为( )| A. |  | B. |  | C. |  | D. |  |
分析 结合点P的运动,将点P的运动路线分成O→A、A→B、B→C三段位置来进行分析三角形OMP面积的计算方式,通过图形的特点分析出面积变化的趋势,从而得到答案.
解答 解:设∠AOM=α,点P运动的速度为a,
当点P从点O运动到点A的过程中,S=(atcosα)•(atsinα)=a2•cosα•sinα•t2,
由于α及a均为常量,从而可知图象本段应为抛物线,且S随着t的增大而增大;
当点P从A运动到B时,由反比例函数性质可知S=k,保持不变,
故本段图象应为与横轴平行的线段;
当点P从B运动到C过程中,四边形OMPN的长ON=OC不变,宽PN在减小,
故本段图象应该为一段下降的线段;
综上所述,则S关于t的函数图象大致为C,
故选C.
点评 本题考查了反比例函数图象性质、锐角三角函数性质,解题的关键是明确点P在O→A、A→B、B→C三段位置时三角形OMP的面积计算方式.

练习册系列答案
 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案
相关题目
13.新房装修后,甲居民购买家居用品的清单如下表,因污水导致部分信息无法识别,根据下表解决问题:
(1)直接写出a=45,b=35;
(2)甲居民购买了垃圾桶,塑料鞋架各几个?
(3)若甲居民再次购买艺术字画和垃圾桶两种家居用品,共花费150元,则有哪几种不同的购买方案?
| 家居用品名称 | 单价(元) | 数量(个) | 金额(元) |
| 挂钟 | 30 | 2 | 60 |
| 垃圾桶 | 15 | ||
| 塑料鞋架 | 40 | ||
| 艺术字画 | a | 2 | 90 |
| 电热水壶 | 35 | 1 | b |
| 合计 | 8 | 280 | |
(2)甲居民购买了垃圾桶,塑料鞋架各几个?
(3)若甲居民再次购买艺术字画和垃圾桶两种家居用品,共花费150元,则有哪几种不同的购买方案?
10.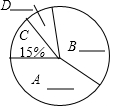 “戒烟一小时,健康亿人行”,今年国际无烟日,某市团委组织人员就公众对在超市吸烟的态度进行了随机抽样调查,主要由四种态度:A.顾客出面制止;B.劝说进吸烟室;C.超市老板出面制止;D.无所谓.他将调查结果绘制了两幅不完整的统计图.请你根据图中的信息回答下列问题:
“戒烟一小时,健康亿人行”,今年国际无烟日,某市团委组织人员就公众对在超市吸烟的态度进行了随机抽样调查,主要由四种态度:A.顾客出面制止;B.劝说进吸烟室;C.超市老板出面制止;D.无所谓.他将调查结果绘制了两幅不完整的统计图.请你根据图中的信息回答下列问题:
请你根据统计图、表提供的信息解答下列问题:
(1)这次抽样的公众有200人.
(2)请将统计表和扇形统计图补充完整;
(3)在统计图中“B”部分所对应的圆心角是126度.
(4)若该市有120万人,估计该市态度为“A.顾客出面制止”的有45万人.
 “戒烟一小时,健康亿人行”,今年国际无烟日,某市团委组织人员就公众对在超市吸烟的态度进行了随机抽样调查,主要由四种态度:A.顾客出面制止;B.劝说进吸烟室;C.超市老板出面制止;D.无所谓.他将调查结果绘制了两幅不完整的统计图.请你根据图中的信息回答下列问题:
“戒烟一小时,健康亿人行”,今年国际无烟日,某市团委组织人员就公众对在超市吸烟的态度进行了随机抽样调查,主要由四种态度:A.顾客出面制止;B.劝说进吸烟室;C.超市老板出面制止;D.无所谓.他将调查结果绘制了两幅不完整的统计图.请你根据图中的信息回答下列问题:| 态度 | A.顾客出面制止 | B.劝说进吸烟室 | C.超市老板出面制止 | D.无所谓 |
| 频数(人数) | 90 | 200 | 30 | 10 |
(1)这次抽样的公众有200人.
(2)请将统计表和扇形统计图补充完整;
(3)在统计图中“B”部分所对应的圆心角是126度.
(4)若该市有120万人,估计该市态度为“A.顾客出面制止”的有45万人.
7.将二次函数y=x2的图象先向下平移1个单位,再向右平移3个单位,得到的图象与一次函数y=2x+b的图象有公共点,则实数b的取值范围是( )
| A. | b>8 | B. | b>-8 | C. | b≥8 | D. | b≥-8 |
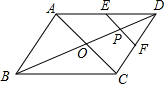 如图,AC、BD相交于点O,且OA=OC=4,OB=OD=6,P是线段BD上一动点,过点P作EF∥AC,与四边形的两条边分别交于点E,F,设BP=x,EF=y,则下列能表示y与x之间函数关系的图象是( )
如图,AC、BD相交于点O,且OA=OC=4,OB=OD=6,P是线段BD上一动点,过点P作EF∥AC,与四边形的两条边分别交于点E,F,设BP=x,EF=y,则下列能表示y与x之间函数关系的图象是( )

 如图所示,AB∥CD∥EF,AC与BD相交于点E,若CE=4,CF=3,AE=BC,则$\frac{CD}{AB}$的值是$\frac{1}{3}$.
如图所示,AB∥CD∥EF,AC与BD相交于点E,若CE=4,CF=3,AE=BC,则$\frac{CD}{AB}$的值是$\frac{1}{3}$.