��Ŀ����
17���Ķ�������ϲ�����й����⣺����֪����|x|=$\left\{\begin{array}{l}{x��x��0��}\\{0��x=0��}\\{-x��x��0��}\end{array}\right.$���������ǿ�������һ�����������о���ֵ�Ĵ���ʽ���������ǿ�������һ�����������о���ֵ�Ĵ���ʽ���绯�����ʽ|x+1|+|x-2|ʱ������x+1=0��x-2=0���ֱ����x=-1��x=2����-1��2�ֱ�Ϊ|x+1|��|x-2|�����ֵ������ʵ����Χ�ڣ����ֵx=-1�ͣ�x=2�ɽ�ȫ��ʵ���ֳɲ��ظ��Ҳ���©������3�������
��x��-1����-1��x��2����x��2��
�Ӷ��������ʽ|x+1|+|x-2|�ɷ�����3�������
�ٵ�x��-1ʱ��ԭʽ=-��x+1��-��x-2��=-2x+1��
�ڵ�-1��x��2ʱ��ԭʽ=x+1-��x-2��=3��
�۵�x��2ʱ��ԭʽ=x+1+x-2=2x-1���������ۣ�ԭʽ=$\left\{\begin{array}{l}{-2x+1��x��-1��}\\{3��-1��x��2��}\\{2x-1��x��2��}\end{array}\right.$��
ͨ�������Ķ����������������⣺
��1���������ʽ|x+2|+|x-4|��
��2����|x-1|-4|x+1|�����ֵ��
���� ��1����Ϊx��-2��-2��x��4��x��4����������ɣ�
��2����x��-1��-1��x��1��x��1�ֱ��x��ȡֵ��Χȷ������ʽֵ�ķ�Χ���Ӷ��������ʽ�����ֵ��
��� �⣺��1����x��-2ʱ��|x+2|+|x-4|=-x-2+4-x=-2x+2��
��-2��x��4ʱ��|x+2|+|x-4|=x+2+4-x=6��
��x��4ʱ��|x+2|+|x-4|=x+2+x-4=2x-2��
��2����x��-1ʱ��ԭʽ=3x+5��2��
��-1��x��1ʱ��ԭʽ=-5x-3��-8��-5x-3��2��
��x��1ʱ��ԭʽ=-3x-5��-8��
��|x-1|-4|x+1|�����ֵΪ2��
���� ������Ҫ�����˾���ֵ������Ĺؼ����ܸ��ݲ���������Ϣ���ҵ����ʵķ������

��ϰ��ϵ�д�
�����Ŀ
6������ȥ������������ȷ�������У�������
| A�� | x-��y-x��=x-y-z | B�� | -��x-y+z��=-x-y-z | ||
| C�� | x+2y-2z=x-2��y-z�� | D�� | -a+c+d+b=-��a-b��+��c+d�� |
7��������y=-3��x-1��2-2�Ŀ��ڷ��Գ���Ͷ��������ǣ�������
| A�� | �������ϣ��Գ���Ϊֱ��x=-1�����㣨-1��-2�� | |
| B�� | �������ϣ��Գ���Ϊֱ��x=1�����㣨1��-2�� | |
| C�� | �������£��Գ���Ϊֱ��x=-1�����㣨1��2�� | |
| D�� | �������£��Գ���Ϊֱ��x=1�����㣨1��-2�� |
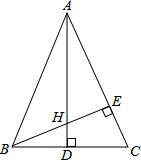 ��֪�ڡ�ABC�У���BAC����ǣ�AB=AC��AD��BE�Ǹߣ���AE=BE����֤��AH=2BD��
��֪�ڡ�ABC�У���BAC����ǣ�AB=AC��AD��BE�Ǹߣ���AE=BE����֤��AH=2BD��