题目内容
7.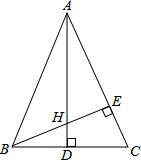 已知在△ABC中,∠BAC是锐角,AB=AC,AD和BE是高,且AE=BE,求证:AH=2BD.
已知在△ABC中,∠BAC是锐角,AB=AC,AD和BE是高,且AE=BE,求证:AH=2BD.
分析 由在△ABC中,AB=AC,∠BAC=45°,可得AE=CE,∠EAH=∠ECB,继而证得△AEH≌△CEB,然后由全等三角形的性质,证得结论.
解答 证明:在△ABC中,
∵∠BAC=45°,CE⊥AB,
∴AE=CE,∠EAH=∠ECB,
在△AEH和△CEB中,
$\left\{\begin{array}{l}{∠EAH=∠ECB}\\{AE=CE}\\{∠AEC=∠BEC=90°}\end{array}\right.$,
∴△AEH≌△CEB(ASA),
∴AH=BC,
∵BC=BD+CD,且BD=CD,
∴BC=2BD,
∴AH=2BD.
点评 此题考查了全等三角形的判定与性质的应用,此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
16.用小木棒按下图方式搭三角形:

观察发现规律并填写下表:

观察发现规律并填写下表:
| 三角形个数 | 1 | 2 | 3 | 4 | … | n |
| 小木棒根数 | 3 | 5 | 7 | 9 | … | 2n+1 |
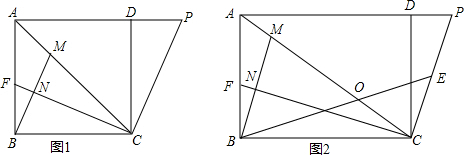
 如图,正方形ABCD中,E为AB上一点,F是BC延长线上一点,且AE=CF,M是EF的中点.
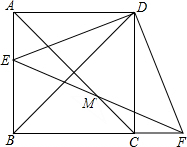
如图,正方形ABCD中,E为AB上一点,F是BC延长线上一点,且AE=CF,M是EF的中点. 如图,△ABC中,AC=6,BC=8,以AB为边向外作正方形ABDE,若此正方形中心为点O,则线段OC长为7$\sqrt{2}$.
如图,△ABC中,AC=6,BC=8,以AB为边向外作正方形ABDE,若此正方形中心为点O,则线段OC长为7$\sqrt{2}$.