题目内容
1.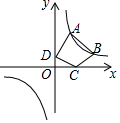 如图,点A(a,3),B(b,1)都在双曲线y=$\frac{3}{x}$上,点C,D,分别是x轴,y轴上的动点,则四边形ABCD周长的最小值为( )
如图,点A(a,3),B(b,1)都在双曲线y=$\frac{3}{x}$上,点C,D,分别是x轴,y轴上的动点,则四边形ABCD周长的最小值为( )| A. | $5\sqrt{2}$ | B. | $6\sqrt{2}$ | C. | $2\sqrt{10}+2\sqrt{2}$ | D. | $8\sqrt{2}$ |
分析 先把A点和B点的坐标代入反比例函数解析式中,求出a与b的值,确定出A与B坐标,再作A点关于y轴的对称点P,B点关于x轴的对称点Q,根据对称的性质得到P点坐标为(-1,3),Q点坐标为(3,-1),PQ分别交x轴、y轴于C点、D点,根据两点之间线段最短得此时四边形PABQ的周长最小,然后利用两点间的距离公式求解可得.
解答 解:分别把点A(a,3)、B(b,1)代入双曲线y=$\frac{3}{x}$得:a=1,b=3,
则点A的坐标为(1,3)、B点坐标为(3,1),
作A点关于y轴的对称点P,B点关于x轴的对称点Q,
所以点P坐标为(-1,3),Q点坐标为(3,-1),
连结PQ分别交x轴、y轴于C点、D点,此时四边形ABCD的周长最小,
四边形ABCD周长=DA+DC+CB+AB
=DP+DC+CQ+AB
=PQ+AB
=$\sqrt{(-1-3)^{2}+(3+1)^{2}}$+$\sqrt{(1-3)^{2}+(3-1)^{2}}$
=4$\sqrt{2}$+2$\sqrt{2}$
=6$\sqrt{2}$,
故选:B.
点评 本题考查了反比例函数的综合题:掌握反比例函数图象上点的坐标特征、熟练运用两点之间线段最短解决有关几何图形周长最短的问题是解题的关键.

练习册系列答案
相关题目
12.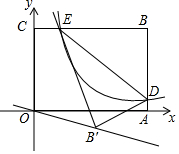 如图,平面直角坐标系xOy中,矩形OABC的边OA、OC分别落在x、y轴上,点B坐标为(6,4),反比例函数y=$\frac{6}{x}$的图象与AB边交于点D,与BC边交于点E,连结DE,将△BDE沿DE翻折至△B'DE处,点B'恰好落在正比例函数y=kx图象上,则k的值是( )
如图,平面直角坐标系xOy中,矩形OABC的边OA、OC分别落在x、y轴上,点B坐标为(6,4),反比例函数y=$\frac{6}{x}$的图象与AB边交于点D,与BC边交于点E,连结DE,将△BDE沿DE翻折至△B'DE处,点B'恰好落在正比例函数y=kx图象上,则k的值是( )
 如图,平面直角坐标系xOy中,矩形OABC的边OA、OC分别落在x、y轴上,点B坐标为(6,4),反比例函数y=$\frac{6}{x}$的图象与AB边交于点D,与BC边交于点E,连结DE,将△BDE沿DE翻折至△B'DE处,点B'恰好落在正比例函数y=kx图象上,则k的值是( )
如图,平面直角坐标系xOy中,矩形OABC的边OA、OC分别落在x、y轴上,点B坐标为(6,4),反比例函数y=$\frac{6}{x}$的图象与AB边交于点D,与BC边交于点E,连结DE,将△BDE沿DE翻折至△B'DE处,点B'恰好落在正比例函数y=kx图象上,则k的值是( )| A. | $-\frac{2}{5}$ | B. | $-\frac{1}{21}$ | C. | $-\frac{1}{5}$ | D. | $-\frac{1}{24}$ |




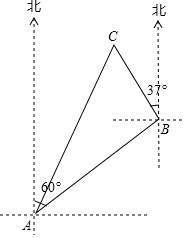 一艘渔船位于港口A的北偏东60°方向,距离港口20海里B处,它沿北偏西37°方向航行至C处突然出现故障,在C处等待救援,B,C之间的距离为10海里,救援船从港口A出发20分钟到达C处,求救援的艇的航行速度.(sin37°≈0.6,cos37°≈0.8,$\sqrt{3}$≈1.732,结果取整数)
一艘渔船位于港口A的北偏东60°方向,距离港口20海里B处,它沿北偏西37°方向航行至C处突然出现故障,在C处等待救援,B,C之间的距离为10海里,救援船从港口A出发20分钟到达C处,求救援的艇的航行速度.(sin37°≈0.6,cos37°≈0.8,$\sqrt{3}$≈1.732,结果取整数)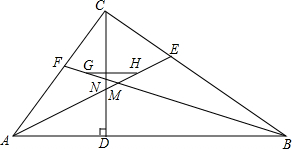 如图Rt△ABC中,∠ACB=90°,AC=3,BC=4,CD⊥AB,AE、BF为角分线,CD与AE相交于M,BF、CD相交于N,H、G分别为EM、FN的中点,求GH的值.
如图Rt△ABC中,∠ACB=90°,AC=3,BC=4,CD⊥AB,AE、BF为角分线,CD与AE相交于M,BF、CD相交于N,H、G分别为EM、FN的中点,求GH的值. 如图,正方形ABCD中,点P是BC边上的任意一点(异于端点B,C),连接AP,过点B,D两点作BE⊥AP于点E,DF⊥AP于点F.
如图,正方形ABCD中,点P是BC边上的任意一点(异于端点B,C),连接AP,过点B,D两点作BE⊥AP于点E,DF⊥AP于点F.