题目内容
6.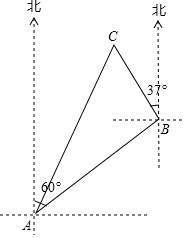 一艘渔船位于港口A的北偏东60°方向,距离港口20海里B处,它沿北偏西37°方向航行至C处突然出现故障,在C处等待救援,B,C之间的距离为10海里,救援船从港口A出发20分钟到达C处,求救援的艇的航行速度.(sin37°≈0.6,cos37°≈0.8,$\sqrt{3}$≈1.732,结果取整数)
一艘渔船位于港口A的北偏东60°方向,距离港口20海里B处,它沿北偏西37°方向航行至C处突然出现故障,在C处等待救援,B,C之间的距离为10海里,救援船从港口A出发20分钟到达C处,求救援的艇的航行速度.(sin37°≈0.6,cos37°≈0.8,$\sqrt{3}$≈1.732,结果取整数)
分析 辅助线如图所示:BD⊥AD,BE⊥CE,CF⊥AF,在Rt△ABD中,根据勾股定理可求AD,在Rt△BCE中,根据三角函数可求CE,EB,在Rt△AFC中,根据勾股定理可求AC,
再根据路程÷时间=速度求解即可.
解答 解:辅助线如图所示: BD⊥AD,BE⊥CE,CF⊥AF,
BD⊥AD,BE⊥CE,CF⊥AF,
有题意知,∠FAB=60°,∠CBE=37°,
∴∠BAD=30°,
∵AB=20海里,
∴BD=10海里,
在Rt△ABD中,AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=10$\sqrt{3}$≈17.32海里,
在Rt△BCE中,sin37°=$\frac{CE}{BC}$,
∴CE=BC•sin37°≈0.6×10=6海里,
∵cos37°=$\frac{EB}{BC}$,
∴EB=BC•cos37°≈0.8×10=8海里,
EF=AD=17.32海里,
∴FC=EF-CE=11.32海里,
AF=ED=EB+BD=18海里,
在Rt△AFC中,
AC=$\sqrt{A{F}^{2}+F{C}^{2}}$=$\sqrt{1{8}^{2}+11.3{2}^{2}}$≈21.26海里,
21.26×3≈64海里/小时.
答:救援的艇的航行速度大约是64海里/小时.
点评 考查了解直角三角形的应用-方向角问题,用到的知识点是方向角、勾股定理、解直角三角形、三角函数值,关键是做出辅助线,构造直角三角形.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
17. 如图,AC⊥BC,CD⊥AB,DE⊥BC,垂足分别为C,D,E,则下列说法不正确的是( )
如图,AC⊥BC,CD⊥AB,DE⊥BC,垂足分别为C,D,E,则下列说法不正确的是( )
 如图,AC⊥BC,CD⊥AB,DE⊥BC,垂足分别为C,D,E,则下列说法不正确的是( )
如图,AC⊥BC,CD⊥AB,DE⊥BC,垂足分别为C,D,E,则下列说法不正确的是( )| A. | DE是△ABE的高 | B. | DE是△BCD的高 | C. | AC是△ABC的高 | D. | AD是△ACD的高 |
14.将点P(2,1)沿x轴方向向左平移3个单位,再沿y轴方向向上平移2个单位,所得的点的坐标是( )
| A. | (5,-1) | B. | (-1,-1) | C. | (-1,3) | D. | (5,3) |
1.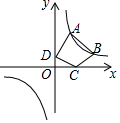 如图,点A(a,3),B(b,1)都在双曲线y=$\frac{3}{x}$上,点C,D,分别是x轴,y轴上的动点,则四边形ABCD周长的最小值为( )
如图,点A(a,3),B(b,1)都在双曲线y=$\frac{3}{x}$上,点C,D,分别是x轴,y轴上的动点,则四边形ABCD周长的最小值为( )
 如图,点A(a,3),B(b,1)都在双曲线y=$\frac{3}{x}$上,点C,D,分别是x轴,y轴上的动点,则四边形ABCD周长的最小值为( )
如图,点A(a,3),B(b,1)都在双曲线y=$\frac{3}{x}$上,点C,D,分别是x轴,y轴上的动点,则四边形ABCD周长的最小值为( )| A. | $5\sqrt{2}$ | B. | $6\sqrt{2}$ | C. | $2\sqrt{10}+2\sqrt{2}$ | D. | $8\sqrt{2}$ |
 如图,分别以正五边形ABCDE的顶点A,D为圆心,以AB长为半径画$\widehat{BE}$,$\widehat{CE}$.若AB=1,则阴影部分图形的周长为$\frac{6}{5}$π+1(结果保留π).
如图,分别以正五边形ABCDE的顶点A,D为圆心,以AB长为半径画$\widehat{BE}$,$\widehat{CE}$.若AB=1,则阴影部分图形的周长为$\frac{6}{5}$π+1(结果保留π). 如图是一块破损的矩形玻璃,只有一条边AB保存完好,现在为了再回收利用这块玻璃,需要在其内部裁出一个以AB为一边的最大矩形,请画出裁痕.(不写作法,保留作图痕迹)
如图是一块破损的矩形玻璃,只有一条边AB保存完好,现在为了再回收利用这块玻璃,需要在其内部裁出一个以AB为一边的最大矩形,请画出裁痕.(不写作法,保留作图痕迹)