题目内容
9.解方程:(1)$\frac{1}{x-2}$+3=$\frac{x-1}{x-2}$
(2)$\frac{x+1}{x-1}$-$\frac{2}{{x}^{2}-1}$=1.
分析 分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:(1)$\frac{1}{x-2}$+3=$\frac{x-1}{x-2}$,
方程两边同乘以(x-2),得:
1+3(x-2)=x-1,
去括号得:1+3x-6=x-1,
称项得:3x-x=-1-1+6,
合并同类项得:2x=4,
系数化为1得:x=2,
经检验:x=2不是原方程的解,
原方程无解;
(2)$\frac{x+1}{x-1}$-$\frac{2}{{x}^{2}-1}$=1,
方程两边同乘以(x-1)(x+1),得:
(x+1)2-2=x2-1,
去括号得:x2+2x+1-2=x2-1,
称项得:2x=-1-1+2,
合并同类项得:2x=0,
系数化为1得:x=0,
经检验:x=0是原方程的解,
∴原方程的解为:x=0.
点评 此题考查了解分式方程,利用了转化的思想,解分式方程注意要检验.

练习册系列答案
相关题目
17. 如图,AC⊥BC,CD⊥AB,DE⊥BC,垂足分别为C,D,E,则下列说法不正确的是( )
如图,AC⊥BC,CD⊥AB,DE⊥BC,垂足分别为C,D,E,则下列说法不正确的是( )
 如图,AC⊥BC,CD⊥AB,DE⊥BC,垂足分别为C,D,E,则下列说法不正确的是( )
如图,AC⊥BC,CD⊥AB,DE⊥BC,垂足分别为C,D,E,则下列说法不正确的是( )| A. | DE是△ABE的高 | B. | DE是△BCD的高 | C. | AC是△ABC的高 | D. | AD是△ACD的高 |
14.将点P(2,1)沿x轴方向向左平移3个单位,再沿y轴方向向上平移2个单位,所得的点的坐标是( )
| A. | (5,-1) | B. | (-1,-1) | C. | (-1,3) | D. | (5,3) |
1.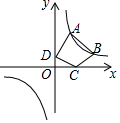 如图,点A(a,3),B(b,1)都在双曲线y=$\frac{3}{x}$上,点C,D,分别是x轴,y轴上的动点,则四边形ABCD周长的最小值为( )
如图,点A(a,3),B(b,1)都在双曲线y=$\frac{3}{x}$上,点C,D,分别是x轴,y轴上的动点,则四边形ABCD周长的最小值为( )
 如图,点A(a,3),B(b,1)都在双曲线y=$\frac{3}{x}$上,点C,D,分别是x轴,y轴上的动点,则四边形ABCD周长的最小值为( )
如图,点A(a,3),B(b,1)都在双曲线y=$\frac{3}{x}$上,点C,D,分别是x轴,y轴上的动点,则四边形ABCD周长的最小值为( )| A. | $5\sqrt{2}$ | B. | $6\sqrt{2}$ | C. | $2\sqrt{10}+2\sqrt{2}$ | D. | $8\sqrt{2}$ |
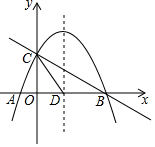 如图,抛物线y=-$\frac{1}{2}$x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(-1,0),C(0,2),点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当四边形CDBF的面积最大时,E点的坐标为(2,1).
如图,抛物线y=-$\frac{1}{2}$x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(-1,0),C(0,2),点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当四边形CDBF的面积最大时,E点的坐标为(2,1).