题目内容
5.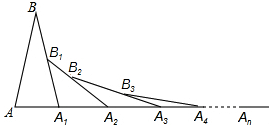 如图,已知AB=A1B,A1B1=A1A2,A2B2=A2A3,A3B3=A3A4…,若∠A=70°,则∠An-1AnBn-1(n>2)的度数为( )
如图,已知AB=A1B,A1B1=A1A2,A2B2=A2A3,A3B3=A3A4…,若∠A=70°,则∠An-1AnBn-1(n>2)的度数为( )| A. | $\frac{70}{{2}^{n}}$ | B. | $\frac{70}{{2}^{n+1}}$ | C. | $\frac{70}{{2}^{n-1}}$ | D. | $\frac{70}{{2}^{n+2}}$ |
分析 根据三角形外角的性质及等腰三角形的性质分别求出∠B1A2A1,∠B2A3A2及∠B3A4A3的度数,找出规律即可得出∠An-1AnBn-1的度数.
解答 解:∵在△ABA1中,∠A=70°,AB=A1B,
∴∠BA1A=70°,
∵A1A2=A1B1,∠BA1A是△A1A2B1的外角,
∴∠B1A2A1=$\frac{∠B{A}_{1}A}{2}$=35°;
同理可得,
∠B2A3A2=17.5°,∠B3A4A3=$\frac{1}{2}$×17.5°=$\frac{35°}{4}$,
∴∠An-1AnBn-1=$\frac{70°}{{2}^{n-1}}$.
故选:C.
点评 本题考查的是等腰三角形的性质及三角形外角的性质,根据题意得出∠B1C2A1,∠B2A3A2及∠B3A4A3的度数,找出规律是解答此题的关键.

练习册系列答案
相关题目
16.已知点A(0,2),B(4,4),点M在x轴上,当AM+BM最小时,点M的坐标为( )
| A. | (1,0) | B. | ($\frac{4}{3}$,0) | C. | ($\sqrt{2}$,0) | D. | (2,0) |
20.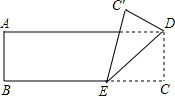 如图,将一张矩形纸片ABCD折叠,使顶点C落在C′处,测量得AB=4,DE=8,则sin∠C′ED为( )
如图,将一张矩形纸片ABCD折叠,使顶点C落在C′处,测量得AB=4,DE=8,则sin∠C′ED为( )
 如图,将一张矩形纸片ABCD折叠,使顶点C落在C′处,测量得AB=4,DE=8,则sin∠C′ED为( )
如图,将一张矩形纸片ABCD折叠,使顶点C落在C′处,测量得AB=4,DE=8,则sin∠C′ED为( )| A. | 2 | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
14.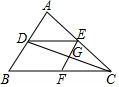 如图,DE∥BC,EF∥AB,则下列结论错误的是( )
如图,DE∥BC,EF∥AB,则下列结论错误的是( )
 如图,DE∥BC,EF∥AB,则下列结论错误的是( )
如图,DE∥BC,EF∥AB,则下列结论错误的是( )| A. | $\frac{EG}{AD}$=$\frac{CE}{CA}$ | B. | $\frac{EC}{EA}$=$\frac{CF}{BF}$ | C. | $\frac{DG}{GC}$=$\frac{DE}{FC}$ | D. | $\frac{CG}{DG}$=$\frac{CF}{AE}$ |
 如图,将小正方体切去一个角后再展开,其平面展开图正确的是( )
如图,将小正方体切去一个角后再展开,其平面展开图正确的是( )



 如图,在等腰三角形ABC中,∠ACB=90°,O是AC中点,D在OB上,且OA=OD,AD的延长线交BC于E,连接CD.
如图,在等腰三角形ABC中,∠ACB=90°,O是AC中点,D在OB上,且OA=OD,AD的延长线交BC于E,连接CD. 如图所示,四边形ABCD内接于⊙O,∠ABC=115°,则∠AOC的度数为130度.
如图所示,四边形ABCD内接于⊙O,∠ABC=115°,则∠AOC的度数为130度.