题目内容
14.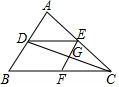 如图,DE∥BC,EF∥AB,则下列结论错误的是( )
如图,DE∥BC,EF∥AB,则下列结论错误的是( )| A. | $\frac{EG}{AD}$=$\frac{CE}{CA}$ | B. | $\frac{EC}{EA}$=$\frac{CF}{BF}$ | C. | $\frac{DG}{GC}$=$\frac{DE}{FC}$ | D. | $\frac{CG}{DG}$=$\frac{CF}{AE}$ |
分析 根据平行线分线段成比例定理和相似三角形的性质逐个判断即可.
解答 解:A、∵EF∥AB,
∴△CEG∽△CAD,
∴$\frac{EG}{AD}$=$\frac{CE}{CA}$,故本选项不符合题意;
B、∵EF∥AB,
∴$\frac{EC}{EA}$=$\frac{CF}{BF}$,故本选项不符合题意;
C、∵DE∥BC,
∴△DEG∽△CFG,
∴$\frac{DG}{GC}$=$\frac{DE}{FC}$,故本选项不符合题意;
D、∵EF∥AB,
∴$\frac{CG}{DG}$=$\frac{CF}{BF}$,
根据已知条件不能推出BF和AE相等,故本选项符合题意;
故选D.
点评 本题考查了平行线分线段成比例定理和相似三角形的性质和判定定理,能得出正确的比例式是解此题的关键.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
5.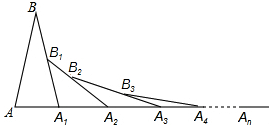 如图,已知AB=A1B,A1B1=A1A2,A2B2=A2A3,A3B3=A3A4…,若∠A=70°,则∠An-1AnBn-1(n>2)的度数为( )
如图,已知AB=A1B,A1B1=A1A2,A2B2=A2A3,A3B3=A3A4…,若∠A=70°,则∠An-1AnBn-1(n>2)的度数为( )
 如图,已知AB=A1B,A1B1=A1A2,A2B2=A2A3,A3B3=A3A4…,若∠A=70°,则∠An-1AnBn-1(n>2)的度数为( )
如图,已知AB=A1B,A1B1=A1A2,A2B2=A2A3,A3B3=A3A4…,若∠A=70°,则∠An-1AnBn-1(n>2)的度数为( )| A. | $\frac{70}{{2}^{n}}$ | B. | $\frac{70}{{2}^{n+1}}$ | C. | $\frac{70}{{2}^{n-1}}$ | D. | $\frac{70}{{2}^{n+2}}$ |
19.七年级(1)班买了若干本4元及7元的笔记本作为奖品,共花费40元,则这两种笔记本的数量可能相差( )
| A. | 1 | B. | 4 | C. | 1或4 | D. | 不确定 |
6.小明借到一本有87页的图书,要在10天之内读完,开始两天每天只读5页,那么以后几天里平均每天至少要读多少页才能读完?设以后几天里平均每天要读x页,所列不等式为( )
| A. | 2+10x≥87 | B. | 2+10x≤87 | C. | 10+8x≤87 | D. | 10+8x≥87 |
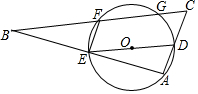 如图,已知ED为⊙O的直径且ED=4,点A(不与E、D重合)为⊙O上一个动点,线段AB经过点E,且EA=EB,F为⊙O上一点,∠FEB=90°,BF的延长线交AD的延长线交于点C.
如图,已知ED为⊙O的直径且ED=4,点A(不与E、D重合)为⊙O上一个动点,线段AB经过点E,且EA=EB,F为⊙O上一点,∠FEB=90°,BF的延长线交AD的延长线交于点C.