题目内容
20．
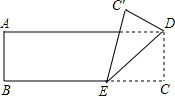如图，将一张矩形纸片ABCD折叠，使顶点C落在C′处，测量得AB=4，DE=8，则sin∠C′ED为（ ）| A． | 2 | B． | $\frac{1}{2}$ | C． | $\frac{\sqrt{2}}{2}$ | D． | $\frac{\sqrt{3}}{2}$ |
分析 由折叠可知，C′D=CD．根据在直角三角形中，一条直角边等于斜边的一半，那么这条直角边所对的锐角等于30°，由特殊角的三角函数选择答案．
解答 解：解：∵△CDE≌△C′DE，
∴C′D=CD．
∵AB=4，DE=8，
∴C′D=4．
∴sin∠C'ED=$\frac{C'D}{ED}$=$\frac{4}{8}$=$\frac{1}{2}$．
故选B．
点评 本题可以考查锐角三角函数的定义及运用：在直角三角形中，锐角的正弦为对边比斜边．
练习册系列答案
口算题天天练系列答案
相关题目
11．线段CD是由线段AB平移得到的，点A（4，7）的对应点为C（-1，4），则点B（-4，-1）的对应点D的坐标为（ ）
| A． | （-9，-4） | B． | （-1，-2） | C． | （2，9） | D． | （5，3） |
如图，灯塔A在港口P的南偏东45°方向，距离港口20$\sqrt{2}$海里处，一艘客轮从港口P出发，沿北偏东30°方向，以20海里/小时的速度驶离港口，客轮出发后几小时后在灯塔的正北方向，并求出此时客轮距灯塔的距离．
5．
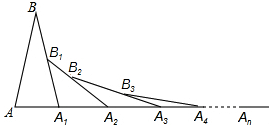如图，已知AB=A1B，A1B1=A1A2，A2B2=A2A3，A3B3=A3A4…，若∠A=70°，则∠An-1AnBn-1（n＞2）的度数为（ ）
如图，已知AB=A1B，A1B1=A1A2，A2B2=A2A3，A3B3=A3A4…，若∠A=70°，则∠An-1AnBn-1（n＞2）的度数为（ ）| A． | $\frac{70}{{2}^{n}}$ | B． | $\frac{70}{{2}^{n+1}}$ | C． | $\frac{70}{{2}^{n-1}}$ | D． | $\frac{70}{{2}^{n+2}}$ |
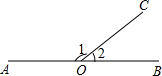如图，点O在直线AB上，OC为射线，∠1比∠2的3倍少10°，设∠1、∠2的度数分别为x、y，则可列方程组为$\left\{\begin{array}{l}{x+y=180°}\\{x=3y-10°}\end{array}\right.$．