题目内容
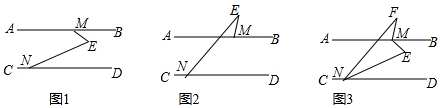
8.如图,已知直线AB∥CD,M、N分别是直线AB和CD上的点.(1)在图1中,判断∠BME、∠MEN和∠DNE之间的数量关系,并证明你的结论.
(2)在图2中,请直接写出∠BME、∠MEN和∠DNE之间的数量关系.(不必证明)
(3)在图3中,MB平分∠EMF,NE平分∠DNF,且∠F与2∠E互补,求∠FME的度数.
分析 (1)过点E作EF∥AB,根据两直线平行,内错角相等可得∠BME=∠1,∠END=∠2,然后相加即可得解;
(2)先根据两直线平行,同位角相等求出∠3=∠END,再根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解;
(3)设∠END=x°,∠BME=y°,根据(1)的结论可得x+y=∠E,根据(2)的结论可得2x+∠F=y,再根据2∠E+∠F=180°,求出y即可.
解答 解:(1)如图1,过点E作EF∥AB,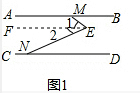
∵AB∥CD,
∴AB∥EF∥CD,
∴∠BME=∠1,∠END=∠2,
∴∠1+∠2=∠BME+∠END,
即∠MEN=∠BME+∠END,
(2)如图2,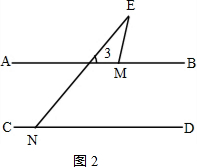
∵AB∥CD,
∴∠3=∠END,
∴∠BME=∠3+∠MEN=∠MEN+∠END,
即∠BME=∠MEN+∠END;
(3)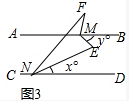
如图3,∵MB平分∠EMF,NE平分∠DNF,
∴∠BMF=∠BME=$\frac{1}{2}$∠EMF,∠DNE=∠FNE=$\frac{1}{2}$∠DNF,
设∠END=x°,∠BME=y°,
由(1)的结论可得∠E=x+y,
由(2)的结论可得:2x+∠F=y,即∠F=-2x+y,
∵∠F+2∠E=180°,
∴-2x+y+2(x+y)=180,
解得:y=60,
∴∠EMF=2y=120°.
点评 本题考查了平行线的性质、三角形的一个外角等于与它不相邻的两个内角的和的性质、角平分线的定义,过拐点作平行线是解题的关键,准确识图理清图中各角度之间的关系也很重要.

练习册系列答案
 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
3.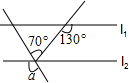 如图,已知直线l1∥l2,则α为( )
如图,已知直线l1∥l2,则α为( )
 如图,已知直线l1∥l2,则α为( )
如图,已知直线l1∥l2,则α为( )| A. | 100° | B. | 120° | C. | 130° | D. | 150° |
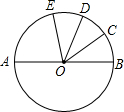 如图,AB是⊙O的直径,$\widehat{BC}$=$\widehat{CD}$=$\widehat{DE}$,∠COD=35°,求∠AOE的度数.
如图,AB是⊙O的直径,$\widehat{BC}$=$\widehat{CD}$=$\widehat{DE}$,∠COD=35°,求∠AOE的度数.