题目内容
4．
如图所示，已知四边形AOBC的各个顶点坐标分别为A（2，10），O（0，0），B（8，0），C（7，8），这个四边形的面积．
分析 首先将四边形OABC分割成两个三角形和一个梯形，利用点的坐标，求出各个线段的对应长度，进而求出面积．
解答 
解：过A作AE⊥OB于E，过C作CF⊥OB于F，
∵A（2，10），O（0，0），B（8，0），C（7，8），
∴OE=2，AE=10，OF=7，BF=1，EF=5，
∴S四边形OBCA=S△AOE+S四边形AEFC+S△BCF=$\frac{1}{2}×2×10$+$\frac{1}{2}（10+8）×5$+$\frac{1}{2}×1×8$=59．
点评 本题考查了直角坐标系中图形面积的求解，解决此类问题关键是将不规则图形分割成可以求解的图形，另外需要注意运算的正确性．
练习册系列答案
轻松暑假总复习系列答案
相关题目
如图，△ABC中，BD平分∠ABC，BC的中垂线交BC于点E，交BD于点F，连接CF．若∠A=60°，∠ABD=24°，则∠ACF=48°．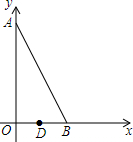
如图，在平面直角坐标系xOy中，点A在y轴上，点B在x轴上，∠ABO=60°，若点D（1，0）且BD=2OD．把△ABO绕着点D逆时针旋转m°（0＜m＜180）后，点B恰好落在初始Rt△ABO的边上，此时的点B记为B′，则点B′的坐标为（2，$\sqrt{3}$）或（0，$\sqrt{3}$）．
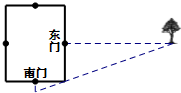《九章算术》是中国传统数学最重要的著作，奠定了中国传统数学的基本框架．其中卷第九勾股，主要讲述了以测量问题为中心的直角三角形三边互求的关系．其中记载：“今有邑，东西七里，南北九里，各中开门，出东门一十五里有木，问：出南门几何步而见木？”
（1）写出图中A，B，C各点的坐标；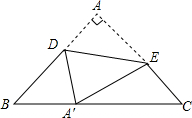
如图，已知△ABC中，∠A=90°，AB=AC，AB=3+3$\sqrt{2}$，点D在AB上，点E在AC上，△ADE沿DE折叠后点A恰好落在BC上的A′点，且DA′⊥BC．则A′B的长是3．