题目内容
16.若(a+b)2=m,(a-b)2=n,用含m、n的式子表示:(1)a2+b2;
(2)ab.
分析 (1)首先利用完全平方公式展开,进而将两式相加得出答案;
(2)利用(1)中所求得出答案.
解答 解:∵(a+b)2=m,(a-b)2=n,
∴a2+b2+2ab=m①,a2+b2-2ab=n②,
(1)①+②得:
2(a2+b2)=m+n,
则a2+b2=$\frac{m+n}{2}$;
(2)由(1)得:$\frac{m+n}{2}$+2ab=m,
解得:ab=$\frac{m-n}{4}$.
点评 此题主要考查了完全平方公式,正确记忆公式是解题关键.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
6.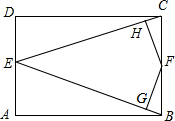 如图,在矩形ABCD中,AB=3,BC=2,点E为AD中点,点F为BC边上任一点,过点F分别作EB,EC的垂线,垂足分别为点G,H,则FG+FH为( )
如图,在矩形ABCD中,AB=3,BC=2,点E为AD中点,点F为BC边上任一点,过点F分别作EB,EC的垂线,垂足分别为点G,H,则FG+FH为( )
 如图,在矩形ABCD中,AB=3,BC=2,点E为AD中点,点F为BC边上任一点,过点F分别作EB,EC的垂线,垂足分别为点G,H,则FG+FH为( )
如图,在矩形ABCD中,AB=3,BC=2,点E为AD中点,点F为BC边上任一点,过点F分别作EB,EC的垂线,垂足分别为点G,H,则FG+FH为( )| A. | $\frac{5}{2}$ | B. | $\frac{5}{2}$$\sqrt{10}$ | C. | $\frac{3}{10}$$\sqrt{10}$ | D. | $\frac{3}{5}$$\sqrt{10}$ |
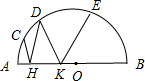 如图,AB是⊙O的直径,C、D、E是⊙O上的点,H、K是直径AB上的点,若∠AHC=∠DHB,∠DKA=∠EKB,$\widehat{AC}$的度数是20°,$\widehat{BE}$的度数是50°,则∠D=55°.
如图,AB是⊙O的直径,C、D、E是⊙O上的点,H、K是直径AB上的点,若∠AHC=∠DHB,∠DKA=∠EKB,$\widehat{AC}$的度数是20°,$\widehat{BE}$的度数是50°,则∠D=55°.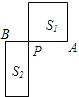 如图,线段AB=1,P是AB的黄金分割点,且PA>PB,S1表示以PA为边长的正方形面积,S2表示以AB为长、PB为宽的矩形面积,则S1-S2=0.
如图,线段AB=1,P是AB的黄金分割点,且PA>PB,S1表示以PA为边长的正方形面积,S2表示以AB为长、PB为宽的矩形面积,则S1-S2=0.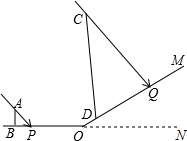 在一个阳光明媚的上午,数学陈老师组织学生测量小山坡的一颗大树CD的高度,山坡OM与地面ON的夹角为30°(∠MON=30°),站立在水平地面上身高1.7米的小明AB在地面的影长BP为1.2米,此刻大树CD在斜坡的影长DQ为5米,求大树的高度.
在一个阳光明媚的上午,数学陈老师组织学生测量小山坡的一颗大树CD的高度,山坡OM与地面ON的夹角为30°(∠MON=30°),站立在水平地面上身高1.7米的小明AB在地面的影长BP为1.2米,此刻大树CD在斜坡的影长DQ为5米,求大树的高度.