Question

4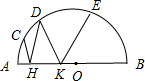．如图，AB是⊙O的直径，C、D、E是⊙O上的点，H、K是直径AB上的点，若∠AHC=∠DHB，∠DKA=∠EKB，$\widehat{AC}$的度数是20°，$\widehat{BE}$的度数是50°，则∠D=55°．

Answer 1

分析 如果将半圆O补全，得圆O．过点D作DF⊥AB于P，交⊙O于F，连接HF、FK．首先由垂径定理，可得DP=FP，则AB是DF的垂直平分线，由线段的垂直平分线的性质得出HD=HF，KD=KF，再由等腰三角形的性质可得∠HDF=∠HFD，∠KDF=∠KFD．然后根据平角的定义证明C、H、F三点共线，E、K、F三点共线．从而∠HDK=∠CFE，最后由圆周角定理求出∠HDK的度数．

解答 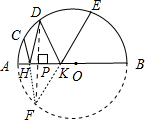解：将半圆O补全，得圆O．过点D作DF⊥AB于P，交⊙O于F，连接HF、FK．
∵DF⊥AB于P，AB是圆O的直径，
∴DP=FP，
∴AB是DF的垂直平分线，
∴HD=HF，KD=KF，
∴∠HDF=∠HFD，∠KDF=∠KFD．
∵HD=HF，DP=FP，
∴∠FHB=∠DHB，
∵∠AHC=∠DHB，
∴∠FHB=∠AHC，
∴∠AHC+∠AHF=∠FHB+∠AHF=180°，
∴C、H、F三点共线．
同理，E、K、F三点共线．
∴∠HDK=∠HDF+∠KDF=∠HFD+∠KFD=∠CFE，
又∵弧AC为20°，弧BE为50°，
∴弧CE为180°-20°-50°=110°，
∴∠CFE=$\frac{1}{2}$×110°=55°，
∴∠HDK=55°．
故答案为：55°．

点评 本题主要考查了垂径定理，线段垂直平分线、等腰三角形的性质，圆周角定理及三点共线的证明方法．综合性强，有一定难度．