题目内容
6.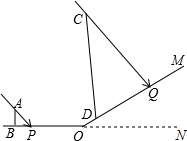 在一个阳光明媚的上午,数学陈老师组织学生测量小山坡的一颗大树CD的高度,山坡OM与地面ON的夹角为30°(∠MON=30°),站立在水平地面上身高1.7米的小明AB在地面的影长BP为1.2米,此刻大树CD在斜坡的影长DQ为5米,求大树的高度.
在一个阳光明媚的上午,数学陈老师组织学生测量小山坡的一颗大树CD的高度,山坡OM与地面ON的夹角为30°(∠MON=30°),站立在水平地面上身高1.7米的小明AB在地面的影长BP为1.2米,此刻大树CD在斜坡的影长DQ为5米,求大树的高度.
分析 根据题意过点Q作QE⊥DC于点E,由题意可得:△ABP∽△CEQ,进而得出EQ,DE,EC的长,即可得出答案.
解答  解:过点Q作QE⊥DC于点E,
解:过点Q作QE⊥DC于点E,
由题意可得:△ABP∽△CEQ,
则$\frac{AB}{BP}$=$\frac{EC}{EQ}$,故$\frac{1.7}{1.2}$=$\frac{EC}{EQ}$,
可得:EQ∥NO,
则∠1=∠2=30°,
∵QD=5m,
∴DE=$\frac{5}{2}$m,EQ=$\frac{5\sqrt{3}}{2}$m,
故$\frac{1.7}{1.2}$=$\frac{EC}{EQ}$=$\frac{EC}{\frac{5\sqrt{3}}{2}}$,
解得:EC=$\frac{85\sqrt{3}}{24}$,
故CE+DE=$\frac{5}{2}$+$\frac{85\sqrt{3}}{24}$=$\frac{60+85\sqrt{3}}{24}$(m),
答:大树的高度为$\frac{60+85\sqrt{3}}{24}$m.
点评 此题主要考查了平行投影以及解直角三角形的应用,根据题意得出EQ的长是解题关键.

练习册系列答案
相关题目
14. 如图所示的几何体的三视图中,面积最大的为( )
如图所示的几何体的三视图中,面积最大的为( )
 如图所示的几何体的三视图中,面积最大的为( )
如图所示的几何体的三视图中,面积最大的为( )| A. | 主视图 | B. | 左视图 | C. | 俯视图 | D. | 一样大 |
1.下列方程是二元一次方程的是( )
| A. | xy=3 | B. | $\frac{x}{2}$+$\frac{y}{2}$=3 | C. | $\frac{2}{x}$+$\frac{2}{y}$=3 | D. | 2x+$\frac{2}{y}$=3 |
11.在0,-2,1,5这四个数中,最小的数是( )
| A. | 0 | B. | -2 | C. | 1 | D. | 5 |
15.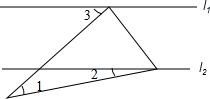 如图,一个直角三角尺的直角顶点和一个锐角顶点分别落在直线l1和l2上,且l1∥l2,∠1=30°,当∠2=10°时,∠3的度数是( )
如图,一个直角三角尺的直角顶点和一个锐角顶点分别落在直线l1和l2上,且l1∥l2,∠1=30°,当∠2=10°时,∠3的度数是( )
 如图,一个直角三角尺的直角顶点和一个锐角顶点分别落在直线l1和l2上,且l1∥l2,∠1=30°,当∠2=10°时,∠3的度数是( )
如图,一个直角三角尺的直角顶点和一个锐角顶点分别落在直线l1和l2上,且l1∥l2,∠1=30°,当∠2=10°时,∠3的度数是( )| A. | 45° | B. | 40° | C. | 35° | D. | 30° |
 如图,正三角形ABC的边长是2,分别以点B,C为圆心,以r为半径作两条弧,设两弧与边BC围成的阴影部分面积为S,当r=$\sqrt{2}$时,S为$\frac{π}{2}$-1.
如图,正三角形ABC的边长是2,分别以点B,C为圆心,以r为半径作两条弧,设两弧与边BC围成的阴影部分面积为S,当r=$\sqrt{2}$时,S为$\frac{π}{2}$-1.