题目内容
某洗衣机经过连续两次降价，每台售价由原来的1500元降到了990元．设平均每次降价的百分率为x，则下列方程中正确的是（ ）
| A、1500（1+x）2=990 |
| B、990（1+x）2=1500 |
| C、1500（1-x）2=990 |
| D、990（1-x）2=1500 |
考点：由实际问题抽象出一元二次方程
专题：增长率问题
分析：本题可先列出第一次降价的售价的代数式，再根据第一次的售价列出第二次降价的售价的代数式，然后根据已知条件即可列出方程．
解答：解：依题意得：第一次降价的售价为：1500（1-x），
则第二次降价后的售价为：1500（1-x）（1-x）=1500（1-x）2，
∴1500（1-x）2=990．
故选C．
则第二次降价后的售价为：1500（1-x）（1-x）=1500（1-x）2，
∴1500（1-x）2=990．
故选C．
点评：本题考查的是一元二次方程的运用，要注意题意指明的是降价，应该是1-x而不是1+x．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
一工厂生产销售某种电子产品，11月份销售电子产品的利润（每台电子产品的利润=出厂价-成本）是出厂价的30%；12月将每台电子产品的出厂价调低5%（每台电子产品的成本不变），销售件数比11月增加44%，那么该厂12月份销售这种电子产品的利润总额将比11月份利润总额增长（ ）
| A、10% | B、15% |
| C、20% | D、25% |
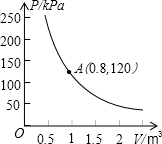某种气球内充满了一定质量的气体，当温度不变时，气球内气体的气压P（kPa）是气体体积V（m3）的反比例函数，其图象如图所示．当气球内气体的气压大于150kPa时，气球将爆炸．为了安全，气体体积V应该是（ ）| A、小于0.64m3 |
| B、大于0.64m3 |
| C、不小于0.64m3 |
| D、不大于0.64m3 |
我国明代珠算家程大位的名著《直指算法统宗》里有一道著名算题：“有100个和尚分100只馒头正好分完．如果大和尚一人分3只小和尚3人分一只，试问大、小和尚各有几人？”请算算大和尚有（ ）
| A、25人 | B、30人 |
| C、50人 | D、75人 |
下列实数中是无理数的是（ ）
A、
| ||
| B、π | ||
| C、0.141414 | ||
D、-
|