题目内容
我国明代珠算家程大位的名著《直指算法统宗》里有一道著名算题:“有100个和尚分100只馒头正好分完.如果大和尚一人分3只小和尚3人分一只,试问大、小和尚各有几人?”请算算大和尚有( )
| A、25人 | B、30人 |
| C、50人 | D、75人 |
考点:一元一次方程的应用
专题:
分析:设大和尚有x人,则小和尚有(100-x)人,根据“有100个和尚分100只馒头正好分完,大和尚一人分3只小和尚3人分一只”列出方程,解方程即可.
解答:解:设大和尚有x人,则小和尚有(100-x)人,根据题意得
3x+
(100-x)=100,
解得x=25,
100-x=75.
答:大和尚有25人,则小和尚有75人.
故选A.
3x+
| 1 |
| 3 |
解得x=25,
100-x=75.
答:大和尚有25人,则小和尚有75人.
故选A.
点评:本题考查了一元一次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
某城市2012年底已有绿化面积380公顷,经过两年绿化,绿化面积逐年增加,到2014年底增加到480公顷.设绿化面积平均每年的增长率为x,由题意,所列方程正确的是( )
| A、380(1+x)2=480 |
| B、380(1+2x)=480 |
| C、380(1+x)3=480 |
| D、380+380(1+x)+380(1+x)2=480 |
某洗衣机经过连续两次降价,每台售价由原来的1500元降到了990元.设平均每次降价的百分率为x,则下列方程中正确的是( )
| A、1500(1+x)2=990 |
| B、990(1+x)2=1500 |
| C、1500(1-x)2=990 |
| D、990(1-x)2=1500 |
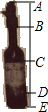 如图所示,的是一种盛装葡萄酒的瓶子,分为瓶塞AB,瓶颈BC,标签CD和瓶底DE四部分,已知;AB:BC=2;3,且DE=
如图所示,的是一种盛装葡萄酒的瓶子,分为瓶塞AB,瓶颈BC,标签CD和瓶底DE四部分,已知;AB:BC=2;3,且DE=