题目内容
3.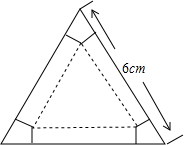 如图,有一块边长为6cm的正三角形纸板.在它的三个顶点处分剐截去一个全等的四边形,再沿图中的虚线折起,做成一个无盖的直三棱柱形纸盒,使它的侧面积等于底面积.求:
如图,有一块边长为6cm的正三角形纸板.在它的三个顶点处分剐截去一个全等的四边形,再沿图中的虚线折起,做成一个无盖的直三棱柱形纸盒,使它的侧面积等于底面积.求:(1)纸盒的高.
(2)截去部分的面积与原三角形纸板面积的比.
分析 (1)设盒子高为xcm,则筝形的长边为$\sqrt{3}$xcm,盒子的底边长为(6-2$\sqrt{3}$x)cm,底面积:$\frac{\sqrt{3}}{4}$(6-2$\sqrt{3}$x)2cm2,侧面积:3x(6-2$\sqrt{3}$x)cm2,根据侧面积等于底面积,列出方程即可求解;
(2)求出当x=$\frac{\sqrt{3}}{3}$时,截去部分的面积和原三角形纸板面积,即可得出结论.
解答 解:(1)设盒子高为xcm,则筝形的长边为$\sqrt{3}$xcm,盒子的底边长为(6-2$\sqrt{3}$x)cm,
底面积:$\frac{\sqrt{3}}{4}$(6-2$\sqrt{3}$x)2cm2,
侧面积:3x(6-2$\sqrt{3}$x)cm2,
则$\frac{\sqrt{3}}{4}$(6-2$\sqrt{3}$x)2=3x(6-2$\sqrt{3}$x),
解得x1=$\frac{\sqrt{3}}{3}$,x2=$\sqrt{3}$(不合题意,舍去);
故盒子高为$\frac{\sqrt{3}}{3}$cm;
(2)当x=$\frac{\sqrt{3}}{3}$时,侧面积=3×$\frac{\sqrt{3}}{3}$×(6-2)=4$\sqrt{3}$cm2,
原等边三角形面积:$\frac{\sqrt{3}}{4}$×62=9$\sqrt{3}$cm2,
剪去面积:9$\sqrt{3}$-8$\sqrt{3}$=$\sqrt{3}$cm2,
∴截去部分的面积与原三角形纸板面积的比=$\sqrt{3}$:9$\sqrt{3}$=1:9.
点评 本题考查了展开图折叠成几何体、等边三角形的性质、折叠的性质以及全等三角形的性质,解题的关键是求出盒子的高.

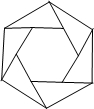 如图,把正六边形各边按同一方向延长,使延长的线段与原正六边形的边长相等,顺次连接这六条线段外端点可以得到一个新的正六边形,…,重复上述过程,经过2018次后,所得到的正六边形边长是原正六边形边长的( )
如图,把正六边形各边按同一方向延长,使延长的线段与原正六边形的边长相等,顺次连接这六条线段外端点可以得到一个新的正六边形,…,重复上述过程,经过2018次后,所得到的正六边形边长是原正六边形边长的( )| A. | ($\sqrt{2}$)2016倍 | B. | ($\sqrt{3}$)2017倍 | C. | ($\sqrt{3}$)2018倍 | D. | ($\sqrt{2}$)2019倍 |
| A. | (π-1)0=0 | B. | 3-2=-6 | C. | (-a)2=a2 | D. | (a3)2=a5 |
 如图,直线y=ax+b(a≠0)与双曲线y=$\frac{k}{x}$(k≠0)交于一、三象限内的A,B两点与x轴交于点C,点A的坐标为(2,m),点B的坐标为(n,-2),tan∠BOC=$\frac{2}{5}$.
如图,直线y=ax+b(a≠0)与双曲线y=$\frac{k}{x}$(k≠0)交于一、三象限内的A,B两点与x轴交于点C,点A的坐标为(2,m),点B的坐标为(n,-2),tan∠BOC=$\frac{2}{5}$.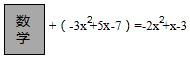
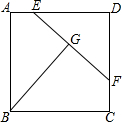 如图,正方形ABCD,点E,F分别在AD,CD上,BG⊥EF,点G为垂足,AB=5,AE=1,CF=2,则BG=$\frac{23}{5}$.
如图,正方形ABCD,点E,F分别在AD,CD上,BG⊥EF,点G为垂足,AB=5,AE=1,CF=2,则BG=$\frac{23}{5}$.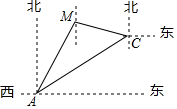 一渔船在海岛A北偏东30°方向的M处遇险,渔船将险情报告给位于A处的救援船后,沿南偏东75°方向向海岛C靠近,同时,从A处出发的救援船沿北偏东60°方向以每小时40$\sqrt{2}$海里的速度匀速航行,30分钟后,救援船在海岛C处恰好追上渔船,那么渔船遇险M处与海岛C的距离是多少海里?($\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7,$\sqrt{6}$≈2.4)
一渔船在海岛A北偏东30°方向的M处遇险,渔船将险情报告给位于A处的救援船后,沿南偏东75°方向向海岛C靠近,同时,从A处出发的救援船沿北偏东60°方向以每小时40$\sqrt{2}$海里的速度匀速航行,30分钟后,救援船在海岛C处恰好追上渔船,那么渔船遇险M处与海岛C的距离是多少海里?($\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7,$\sqrt{6}$≈2.4)