题目内容
15.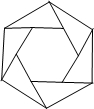 如图,把正六边形各边按同一方向延长,使延长的线段与原正六边形的边长相等,顺次连接这六条线段外端点可以得到一个新的正六边形,…,重复上述过程,经过2018次后,所得到的正六边形边长是原正六边形边长的( )
如图,把正六边形各边按同一方向延长,使延长的线段与原正六边形的边长相等,顺次连接这六条线段外端点可以得到一个新的正六边形,…,重复上述过程,经过2018次后,所得到的正六边形边长是原正六边形边长的( )| A. | ($\sqrt{2}$)2016倍 | B. | ($\sqrt{3}$)2017倍 | C. | ($\sqrt{3}$)2018倍 | D. | ($\sqrt{2}$)2019倍 |
分析 先根据正六边形的性质得出∠1的度数,再根据AD=CD=BC判断出△ABC的形状及∠2的度数,求出AB的长,进而可得出,经过2018次后,即可得出所得到的正六边形的边长.
解答  解:∵此六边形是正六边形,
解:∵此六边形是正六边形,
∴∠1=180°-120°=60°,
∵AD=CD=BC,
∴△BCD为等边三角形,
∴BD=$\frac{1}{2}$AC,
∴△ABC是直角三角形
又∵BC=$\frac{1}{2}$AC,
∴∠2=30°,
∴AB=$\sqrt{3}$BC=$\sqrt{3}$CD,
同理可得,经过2次后,所得到的正六边形是原正六边形边长($\sqrt{3}$)2倍,
∴经过2018次后,所得到的正六边形是原正六边形边长的($\sqrt{3}$)2018,
故选C.
点评 本题考查的是正多边形和圆,解答此题的关键是熟知正多边形内角的性质及直角三角形的判定定理,此题有一定的难度.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
5.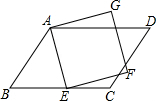 如图,?ABCD中,E为BC边上一点,以AE为边作正方形AEFG,若∠BAE=40°,∠CEF=15°,则∠D的度数是( )
如图,?ABCD中,E为BC边上一点,以AE为边作正方形AEFG,若∠BAE=40°,∠CEF=15°,则∠D的度数是( )
 如图,?ABCD中,E为BC边上一点,以AE为边作正方形AEFG,若∠BAE=40°,∠CEF=15°,则∠D的度数是( )
如图,?ABCD中,E为BC边上一点,以AE为边作正方形AEFG,若∠BAE=40°,∠CEF=15°,则∠D的度数是( )| A. | 65° | B. | 55° | C. | 70° | D. | 75° |
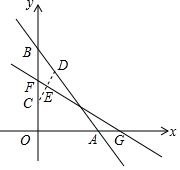 如图,直线y=-$\frac{4}{3}$x+4与x轴、y轴分别相交于点A,B,点C从点O出发沿射线OB方向以每秒1个单位速度运动,同时点D从点B出发沿BA方向以相同的速度向点A运动.当点D到达点A同时停止运动,点C也随之停止.连接CD,过CD的中点E作EF⊥CD交y轴于点F,交x轴于点G,设运动的时间时t秒.
如图,直线y=-$\frac{4}{3}$x+4与x轴、y轴分别相交于点A,B,点C从点O出发沿射线OB方向以每秒1个单位速度运动,同时点D从点B出发沿BA方向以相同的速度向点A运动.当点D到达点A同时停止运动,点C也随之停止.连接CD,过CD的中点E作EF⊥CD交y轴于点F,交x轴于点G,设运动的时间时t秒.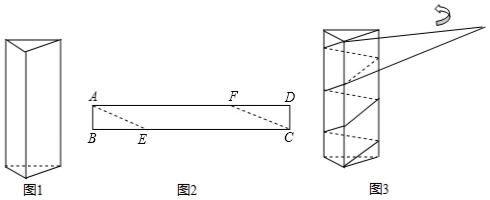
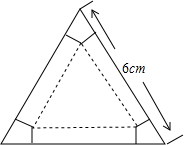 如图,有一块边长为6cm的正三角形纸板.在它的三个顶点处分剐截去一个全等的四边形,再沿图中的虚线折起,做成一个无盖的直三棱柱形纸盒,使它的侧面积等于底面积.求:
如图,有一块边长为6cm的正三角形纸板.在它的三个顶点处分剐截去一个全等的四边形,再沿图中的虚线折起,做成一个无盖的直三棱柱形纸盒,使它的侧面积等于底面积.求: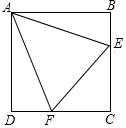 已知正方形ABCD的边长为4,点E,F分别在边BC、CD上,∠EAF=45°,若AE•AF=$\frac{40\sqrt{2}}{3}$,则EF的长为$\frac{10}{3}$.
已知正方形ABCD的边长为4,点E,F分别在边BC、CD上,∠EAF=45°,若AE•AF=$\frac{40\sqrt{2}}{3}$,则EF的长为$\frac{10}{3}$.