题目内容
11.甲驾驶汽车从A地到B地需2小时,乙车骑摩托车从B地到A地需3小时.如果乙先骑摩托车从B地出发前往A地,1小时后甲驾驶汽车从A地出发往B地,那么乙出发$\frac{9}{5}$小时与甲相遇.分析 甲驾驶汽车从A地到B地需2h,乙骑摩托车从B地到A地需3h,则甲速度为$\frac{1}{2}$,乙速度为$\frac{1}{3}$,设甲出发x小时后与乙相遇,则根据乙走1小时后甲出发,根据两者共走路程不变列出方程式即可解题.
解答 解:甲驾驶汽车从A地到B地需2h,乙骑摩托车从B地到A地需3h,则甲速度为$\frac{1}{2}$,乙速度为$\frac{1}{3}$,
设甲出发x小时后与乙相遇,则
$\frac{1}{3}$+($\frac{1}{2}$+$\frac{1}{3}$)x=1,
解得:x=$\frac{4}{5}$,
$\frac{4}{5}$+1=$\frac{9}{5}$(小时).
答:乙出发$\frac{9}{5}$小时与甲相遇.
故答案为:$\frac{9}{5}$.
点评 本题考查了一元一次方程的应用,本题中设甲出发x小时后与乙相遇,根据路程不变的等量关系列出方程式是解题的关键.

练习册系列答案
相关题目
1.“遇见最美春天”,某校组织九年级学生参观绿博园时,在植物园中了解到一种花瓣的花粉颗粒直径约为0.0000065米,0.0000065用科学记数法表示为( )
| A. | 6.5×10-5 | B. | 6.5×10-7 | C. | 6.5×10-6 | D. | 65×10-6 |


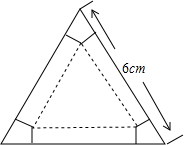 如图,有一块边长为6cm的正三角形纸板.在它的三个顶点处分剐截去一个全等的四边形,再沿图中的虚线折起,做成一个无盖的直三棱柱形纸盒,使它的侧面积等于底面积.求:
如图,有一块边长为6cm的正三角形纸板.在它的三个顶点处分剐截去一个全等的四边形,再沿图中的虚线折起,做成一个无盖的直三棱柱形纸盒,使它的侧面积等于底面积.求: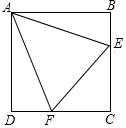 已知正方形ABCD的边长为4,点E,F分别在边BC、CD上,∠EAF=45°,若AE•AF=$\frac{40\sqrt{2}}{3}$,则EF的长为$\frac{10}{3}$.
已知正方形ABCD的边长为4,点E,F分别在边BC、CD上,∠EAF=45°,若AE•AF=$\frac{40\sqrt{2}}{3}$,则EF的长为$\frac{10}{3}$.