题目内容
11.抛物线y=ax2+c与x轴交于A、B两点(A在B的左边),与y轴交于点C,抛物线上有一动点P(1)若A(-2,0),C(0,-4)
①求抛物线的解析式;
②在①的情况下,若点P在第四象限运动,点D(0,-2),以BD、BP为邻边作平行四边形BDQP,求平行四边形BDQP面积的取值范围.
(2)若点P在第一象限运动,且a<0,连接AP、BP分别交y轴于点E、F,则问$\frac{{{S}_{△AOE}+S}_{△BOF}}{{S}_{△ABC}}$是否与a,c有关?若有关,用a,c表示该比值;若无关,求出该比值.
分析 (1)①由A、C两点的坐标,利用待定系数法可求得抛物线解析式;②连接BD、OP,设出P点坐标,利用S△BDP=S△ODP+S△OBP-S△BOD可用x表示出四边形BDQP的面积,借助x的取值范围,可求得四边形BDQP面积的取值范围;
(2)过点P作PG⊥AB,设A(x1,0),B(x2,0),P(x,y),由△AOE∽△AGP、△BGP∽△BOF,利用相似三角形的性质和一元二次方程根与系数的关系可整理得到$\frac{OE+OF}{OC}$=2,再利用三角形的面积可得$\frac{{{S}_{△AOE}+S}_{△BOF}}{{S}_{△ABC}}$的值.
解答 解:
(1)①∵A(-2,0),C(0,-4)在抛物线上,
∴$\left\{\begin{array}{l}{4a+c=0}\\{c=-4}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=1}\\{c=-4}\end{array}\right.$,
∴抛物线解析式为y=x2-4;
②如图1,连接DB、OP,设P(x,x2-4),
∵A(-2,0),对称轴为y轴,
∴B(2,0),
∴S△BDP=S△ODP+S△OBP-S△BOD=$\frac{1}{2}$OD•|x|+$\frac{1}{2}$OB•|x2-4|-$\frac{1}{2}$OD•OB=x+4-x2-2=-x2+x+2=-(x-$\frac{1}{2}$)2+$\frac{9}{4}$,
∵点P在第四象限运动,
∴0<x<2,
∴当x=$\frac{1}{2}$时,S△BDP有最大值$\frac{9}{4}$,当x=2时,S△BDP有最小值0,
∴0<S△BDP≤$\frac{9}{4}$,
∵四边形BDQC为平行四边形,
∴S四边形BDQP=2S△BDP,
∴0<S四边形BDQP≤$\frac{9}{2}$;
(2)如图2,过点P作PG⊥AB,设A(x1,0),B(x2,0),P(x,y),
∵PG∥y轴,
∴△AOE∽△AGP,△BGP∽△BOF,
∴$\frac{AO}{AG}$=$\frac{OE}{GP}$,$\frac{BO}{BG}$=$\frac{OF}{GP}$,
∴$\frac{-{x}_{1}}{x-{x}_{1}}$=$\frac{OE}{y}$,$\frac{{x}_{2}}{{x}_{2}-x}$=$\frac{OF}{y}$,
∴$\frac{OE}{y}$+$\frac{OF}{y}$=$\frac{-{x}_{1}}{x-{x}_{1}}$+$\frac{{x}_{2}}{{x}_{2}-x}$=$\frac{-{x}_{1}({x}_{2}-x)+{x}_{2}(x-{x}_{1})}{(x-{x}_{1})({x}_{2}-x)}$=$\frac{({x}_{1}+{x}_{2})x-2{x}_{1}{x}_{2}}{-{x}^{2}+({x}_{1}+{x}_{2})x-{x}_{1}{x}_{2}}$,
当y=0时,可得ax2+c=0,
∴x1+x2=0,x1x2=$\frac{c}{a}$,
∴$\frac{OE}{y}$+$\frac{OF}{y}$=$\frac{-\frac{2c}{a}}{-{x}^{2}-\frac{c}{a}}$=$\frac{2c}{a{x}^{2}+c}$=$\frac{2c}{y}$,
∴OE+OF=2c,
∴$\frac{OE+OF}{OC}$=$\frac{2c}{c}$=2,
∴$\frac{{{S}_{△AOE}+S}_{△BOF}}{{S}_{△ABC}}$=$\frac{\frac{1}{2}OA•OE+\frac{1}{2}OB•OF}{\frac{1}{2}AB•OC}$=$\frac{\frac{1}{2}OB•(OE+OF)}{\frac{1}{2}•2OB•OC}$=$\frac{OE+OF}{2OC}$=1,
∴$\frac{{{S}_{△AOE}+S}_{△BOF}}{{S}_{△ABC}}$的值与a,c无关,比值为1.
点评 本题为二次函数的综合应用,涉及待定系数法、平行四边形的性质、三角形的面积、一元二次方程根与系数的关系、相似三角形的判定和性质、方程思想及转化思想等知识.在(1)②中用x表示出△BDP的面积是解题的关键,在(2)中利用相似三角形的性质求得OE+OF=2c是解题的关键.本题考查知识点较多,综合性较强,难度较大.

 阅读快车系列答案
阅读快车系列答案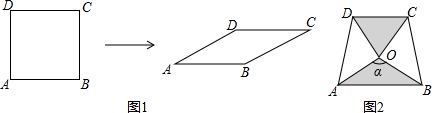
(1)请补全表:
| α | 30° | 45° | 60° | 90° | 120° | 135° | 150° |
| S | $\frac{1}{2}$ | 1 | $\frac{\sqrt{2}}{2}$ |
(3)两块相同的等腰直角三角板按图2的方式放置,AD=$\sqrt{2}$,∠AOB=α,试探究图中两个带阴影的三角形面积是否相等,并说明理由(注:可以利用(2)中的结论).
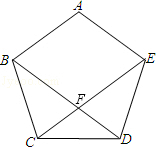 如图,正五边形ABCDE的对角线BD、CE相交于点F,则下列结论正确的是( )
如图,正五边形ABCDE的对角线BD、CE相交于点F,则下列结论正确的是( )| A. | ∠BCE=36° | B. | △BCF是直角三角形 | ||
| C. | △BCD≌△CDE | D. | AB⊥BD |

 如图,将三角形ABC向右平移2个单位长度,再向下平移3个单位长度,得到对应的三角形A1B1C1.
如图,将三角形ABC向右平移2个单位长度,再向下平移3个单位长度,得到对应的三角形A1B1C1.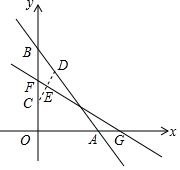 如图,直线y=-$\frac{4}{3}$x+4与x轴、y轴分别相交于点A,B,点C从点O出发沿射线OB方向以每秒1个单位速度运动,同时点D从点B出发沿BA方向以相同的速度向点A运动.当点D到达点A同时停止运动,点C也随之停止.连接CD,过CD的中点E作EF⊥CD交y轴于点F,交x轴于点G,设运动的时间时t秒.
如图,直线y=-$\frac{4}{3}$x+4与x轴、y轴分别相交于点A,B,点C从点O出发沿射线OB方向以每秒1个单位速度运动,同时点D从点B出发沿BA方向以相同的速度向点A运动.当点D到达点A同时停止运动,点C也随之停止.连接CD,过CD的中点E作EF⊥CD交y轴于点F,交x轴于点G,设运动的时间时t秒.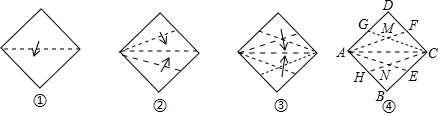
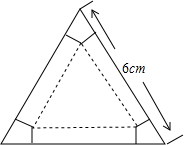 如图,有一块边长为6cm的正三角形纸板.在它的三个顶点处分剐截去一个全等的四边形,再沿图中的虚线折起,做成一个无盖的直三棱柱形纸盒,使它的侧面积等于底面积.求:
如图,有一块边长为6cm的正三角形纸板.在它的三个顶点处分剐截去一个全等的四边形,再沿图中的虚线折起,做成一个无盖的直三棱柱形纸盒,使它的侧面积等于底面积.求: