题目内容
18.老师在黑板上书写了一个正确的演算过程,随后用书遮住了一个多项式,形式如下: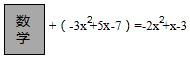
(1)求所遮住的多项式;
(2)若x是$\frac{1}{4}$x=-$\frac{1}{2}$x+3的解,求所遮住的多项式的值;
(3)若x为不小于2的正整数,任取几个值并求出所遮住的多项式的值,你能发现什么规律?
(4)若所遮住的多项式的值为169,请直接写出正整数x的取值.
分析 (1)用-2x2+x-3减去-3x2+5x-7,即可得出答案;
(2)先解方程,再代入计算即可;
(3)先确定x的值,代入计算即可得出规律;
(4)列出方程,再求得正整数x的值即可.
解答 解:(1)所遮住的多项式=(-2x2+x-3)-(-3x2+5x-7)=-2x2+x-3+3x2-5x+7=x2-4x+4;
(2)去分母得,x=-2x+12,
整理得x=4,
把x=4代入x2-4x+4中,原式=16-16+4=4.
故所遮住的多项式的值为4;
(3)当x=1时,x2-4x+4=1-4+4=4;
当x=2时,x2-4x+4=4-8+4=0;
所遮住的多项式的值是完全平方数;
(4)依题意有x2-4x+4=169,
(x+11)(x-15)=0,
解得x1=-11(舍去),x2=15.
故正整数x的取值是15.
点评 考查了整式的加减,一元二次方程的解,解题的关键是求出所遮住的多项式的值.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目
8.某校九年级一班全体学生2017年中招理化生实验操作考试的成绩统计如下表,根据表中的信息判断,下列结论中错误的是( )
| 成绩(分) | 30 | 29 | 28 | 26 | 18 |
| 人数(人) | 32 | 4 | 2 | 1 | 1 |
| A. | 该班共有40名学生 | |
| B. | 该班学生这次考试成绩的平均数为29.4分 | |
| C. | 该班学生这次考试成绩的众数为30分 | |
| D. | 该班学生这次考试成绩的中位数为28分 |
 如图,将三角形ABC向右平移2个单位长度,再向下平移3个单位长度,得到对应的三角形A1B1C1.
如图,将三角形ABC向右平移2个单位长度,再向下平移3个单位长度,得到对应的三角形A1B1C1.
 如图,△ABC在正方形网格中,若小方格的边长均为1,试判断△ABC的形状,并说明理由.
如图,△ABC在正方形网格中,若小方格的边长均为1,试判断△ABC的形状,并说明理由. 如图,有一块边长为6cm的正三角形纸板.在它的三个顶点处分剐截去一个全等的四边形,再沿图中的虚线折起,做成一个无盖的直三棱柱形纸盒,使它的侧面积等于底面积.求:
如图,有一块边长为6cm的正三角形纸板.在它的三个顶点处分剐截去一个全等的四边形,再沿图中的虚线折起,做成一个无盖的直三棱柱形纸盒,使它的侧面积等于底面积.求: