题目内容
19.在平面直角坐标系xOy中,若点P的横坐标和纵坐标相等,则称点P为等值点.例如点(1,1).(-2,-2).($\sqrt{3}$,$\sqrt{3}$),…,都是等值点.已知二次函数y=ax2+4x+c(a≠0)的图象上有且只有一个等值点($\frac{3}{4}$,$\frac{3}{4}$),且当m≤x≤3时,函数y=ax2+4x+c-$\frac{15}{8}$(a≠0)的最小值为-9,最大值为-1,则m的取值范围是-1≤m≤1.分析 根据等值点的概念令ax2+4x+c=x,即ax2+3x+c=0,由题意,△=32-4ac=0,即4ac=9,方程的根为$\frac{-3}{2a}$=$\frac{3}{4}$,从而求得a=-2,c=-$\frac{9}{8}$,所以函数y=ax2+4x+c-$\frac{15}{8}$=-2x2+4x-3,根据函数解析式求得顶点坐标,根据y的取值,即可确定x的取值范围.
解答 解:令ax2+4x+c=x,即ax2+3x+c=0,
由题意,△=32-4ac=0,即4ac=9,
又方程的根为$\frac{-3}{2a}$=$\frac{3}{4}$,
解得a=-2,c=-$\frac{9}{8}$.
故函数y=ax2+4x+c-$\frac{15}{8}$=-2x2+4x-3=-2(x-1)2-1,
如图,该函数图象顶点为(1,-1),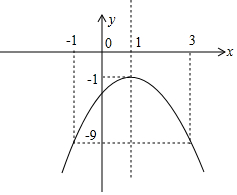
由于函数图象在对称轴x=1左侧y随x的增大而增大,在对称轴右侧y随x的增大而减小,
且当m≤x≤3时,函数y=-2x2+4x-3的最小值为-9,最大值为-1,
∴-1≤m≤1,
故答案为:-1≤m≤1.
点评 本题是二次函数的综合题,考查了二次函数图象上点的坐标特征,二次函数的性质以及根的判别式等知识,利用分类讨论以及数形结合得出是解题关键.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
4.线段MN是由线段EF经过平移得到的,若点E(-1,3)的对应点M(2,5),则点F(-3,-2)的对应点N的坐标是( )
| A. | (0,0) | B. | (-6,0) | C. | (0,-4) | D. | (-1,0) |
11.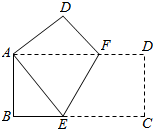 如图,将一个边长分别为4cm、8cm的矩形纸片ABCD折叠,使C点与A点重合,则EB的长是( )
如图,将一个边长分别为4cm、8cm的矩形纸片ABCD折叠,使C点与A点重合,则EB的长是( )
 如图,将一个边长分别为4cm、8cm的矩形纸片ABCD折叠,使C点与A点重合,则EB的长是( )
如图,将一个边长分别为4cm、8cm的矩形纸片ABCD折叠,使C点与A点重合,则EB的长是( )| A. | 3cm | B. | 4cm | C. | 2cm | D. | 5cm |
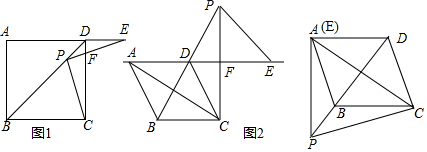
 如图,一次函数y=x+4的图象与反比例函数y=$\frac{k}{x}$(k为常数,且k≠0)的图象交于A(-1,a),B(b,1)两点.
如图,一次函数y=x+4的图象与反比例函数y=$\frac{k}{x}$(k为常数,且k≠0)的图象交于A(-1,a),B(b,1)两点.