题目内容
10．平行四边形ABCD中，有两个内角的比为1：2，则这个平行四边形中较小的内角是60度．分析 根据平行四边形的性质可知，平行四边形的对角相等，邻角互补，故该平行四边形的四个角的比值为1：2：1：2，所以可以计算出平行四边形的各个角的度数．
解答 解：根据平行四边形的相邻的两个内角互补知，设较小的内角的度数为x，
则有：x+2x=180°
∴x=60°，
即较小的内角是60°
故答案为：60．
点评 本题利用了平行四边形的性质，即平行四边形的对角相等，相邻的两个内角互补．
练习册系列答案
阳光课堂课时优化作业系列答案
相关题目
如图，在平面直角坐标系中，点P在函数y=$\frac{3}{x}$（x＞0）的图象上．过点P分别作x轴、y轴的垂线，垂足分别为A、B，取线段OB的中点C，连结PC并延长交x轴于点D，则△APD的面积为3．
15．我县组织20辆汽车装运食品、药品、生活用品三种扶贫物资共100吨到某乡实施扶贫工作，按计划20辆汽车都要装运，每辆汽车只能装运同一种救灾物资且必须装满，根据表中提供的信息，解答下列问题：
（1）设装运食品的车辆数为x，装运药品的车辆数为y．求y与x的函数关系式；
（2）如果装运食品的车辆数不少于5辆，装运药品的车辆数不少于4辆，那么车辆的安排有几种方案？并写出每种安排方案；
（3）在（2）的条件下，若要求总运费最少，应如何安排车辆？并求出最少总运费．
| 物资种类 | 食品 | 药品 | 生活用品 |
| 每辆汽车运载量（吨） | 6 | 5 | 4 |
| 每吨所需运费（元/吨） | 120 | 160 | 100 |
（2）如果装运食品的车辆数不少于5辆，装运药品的车辆数不少于4辆，那么车辆的安排有几种方案？并写出每种安排方案；
（3）在（2）的条件下，若要求总运费最少，应如何安排车辆？并求出最少总运费．
2．
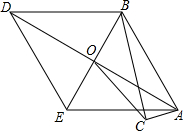如图，在△ABC中，∠ACB=90°，AC=1，BC=2$\sqrt{3}$，以AB为边向左作菱形ABDE，使∠BAE=60°，AD，BE相交于点O，则CO的长是（ ）
如图，在△ABC中，∠ACB=90°，AC=1，BC=2$\sqrt{3}$，以AB为边向左作菱形ABDE，使∠BAE=60°，AD，BE相交于点O，则CO的长是（ ）| A． | $\frac{5}{2}$ | B． | 3 | C． | $\frac{9}{4}$ | D． | $\sqrt{6}$ |
