题目内容
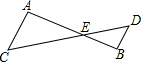如图，已知△ACE∽△BDE，∠A=117°，∠C=37°，AC=6，BD=3，AB=12，CD=18，（1）求∠B和∠D的度数；（2）求AE和DE的长．
考点：相似三角形的性质
专题：
分析：（1）直接根据相似三角形的对应角相等可得出∠B与∠D的度数；
（2）设AE=x，DE=y，则BE=12-x，CE=18-y，再由相似三角形的对应边成比例即可得出结论．
（2）设AE=x，DE=y，则BE=12-x，CE=18-y，再由相似三角形的对应边成比例即可得出结论．
解答：解：（1）∵△ACE∽△BDE，∠A=117°，∠C=37°，
∴∠B=∠A=117°，∠C=∠D=37°；
（2）∵△ACE∽△BDE，AC=6，BD=3，AB=12，CD=18，
∴设AE=x，DE=y，则BE=12-x，CE=18-y，
∴
=
=
，即
=
=
，解得x=8，y=6，
∴AE=8，DE=6．
∴∠B=∠A=117°，∠C=∠D=37°；
（2）∵△ACE∽△BDE，AC=6，BD=3，AB=12，CD=18，
∴设AE=x，DE=y，则BE=12-x，CE=18-y，
∴
| AC |
| BD |
| AE |
| BE |
| CE |
| DE |
| 6 |
| 3 |
| x |
| 12-x |
| 18-y |
| y |
∴AE=8，DE=6．
点评：本题考查的是相似三角形的性质，熟知相似三角形对应角相等，对应边成比例是解答此题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
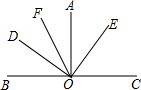如图所示，∠AOB=∠AOC=90°，∠DOE=90°，OF平分∠AOD，∠AOE=36°．
如图，在平面直角坐标系xOy中，正比例函数y=2x与反比例函数y=
如图，在⊙O中，将△OAB绕点O顺时针方向旋转85°，得到△OCD．若∠BAC=15°，则∠BOC的度数为
如图，在△ABC中，∠ABC=∠C，BD平分∠ABC，∠A=36°，则∠BDC=
如图，△ABC中，∠C=90°，点D在AC上，已知∠BDC=45°，CD=10，AB=20，求∠A的度数．
如图，AB⊥BC，AD⊥DC，∠BAD=110°，在BC、CD上分别找一点M、N，当△AMN周长最小时，∠AMN+∠ANM的度数是