题目内容
把抛物线y=-2x2+4x+1沿坐标轴先向左平移2个单位,再向上平移3个单位,向所得的抛物线有没有最大值,若有,求出最大值;若没有,说明理由.
考点:二次函数图象与几何变换
专题:几何变换
分析:先利用配方法得到抛物线的顶点坐标为(1,3),再根据点平移的规律得到点(1,3)平移后所得对应点的坐标为(-1,6),然后根据顶点式写出平移后的抛物线解析式,再利用二次函数的性质解决最大值问题.
解答:解:y=-2x2+4x+1=-2(x-1)2+3,抛物线的顶点坐标为(1,3),把点(1,3)先向左平移2个单位,再向上平移3个单位所得对应点的坐标为(-1,6),所以平移后的抛物线解析式为y=-2(x+1)2+6,
因为a=-2<0,
所以当x=-1时,所得二次函数有最大值,最大值为6.
因为a=-2<0,
所以当x=-1时,所得二次函数有最大值,最大值为6.
点评:本题考查了二次函数与几何变换:由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.

练习册系列答案
相关题目
解为x=0的方程是( )
| A、2x-6=0 | ||||||
| B、3(x-2)-2(x-3)=5x | ||||||
C、
| ||||||
D、
|
 如图,将右边的图案变成左边的图案,是通过
如图,将右边的图案变成左边的图案,是通过

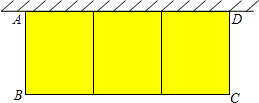 如图,在一面靠墙的空地上用长为24米的篱笆,围成中间隔有二道篱笆的长方形花圃,设花圃的宽AB为x米,面积为S平方米.
如图,在一面靠墙的空地上用长为24米的篱笆,围成中间隔有二道篱笆的长方形花圃,设花圃的宽AB为x米,面积为S平方米.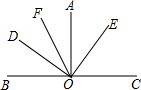 如图所示,∠AOB=∠AOC=90°,∠DOE=90°,OF平分∠AOD,∠AOE=36°.
如图所示,∠AOB=∠AOC=90°,∠DOE=90°,OF平分∠AOD,∠AOE=36°.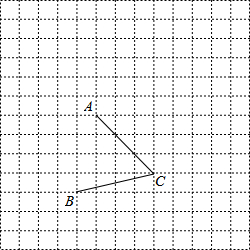 在如图所示的方格纸中,按下列要求画图:
在如图所示的方格纸中,按下列要求画图: 如图,⊙O1、⊙O2外切于点P,A是⊙O1上一点,直线AC切⊙O2于点C,交⊙O1于点B,直线AP交⊙O2于点D.
如图,⊙O1、⊙O2外切于点P,A是⊙O1上一点,直线AC切⊙O2于点C,交⊙O1于点B,直线AP交⊙O2于点D. 如图,△ABC中,∠C=90°,点D在AC上,已知∠BDC=45°,CD=10,AB=20,求∠A的度数.
如图,△ABC中,∠C=90°,点D在AC上,已知∠BDC=45°,CD=10,AB=20,求∠A的度数.