题目内容
6．过多边形的一个顶点的所有对角线把多边形分成4个三角形，这个多边形对角线的总条数是（ ）| A． | 8 | B． | 9 | C． | 10 | D． | 11 |
分析 根据n边形从一个顶点出发可引出（n-3）条对角线，可组成（n-2）个三角形，依此可得n的值，再根据n边形对角线条数=$\frac{n（n-3）}{2}$计算即可．
解答 解：从n边形的一个顶点出发可引出（n-3）条对角线，可组成（n-2）个三角形，
即可得n-2=4，
解得：n=6，
所以多边形对角线总条数为$\frac{n（n-3）}{2}$=$\frac{6×3}{2}$=9
故选B．
点评 本题考查了多边形的对角线，求对角线条数时，直接代入边数n的值计算，而计算边数时，需利用方程思想，解方程求n，记住n边形对角线总条数为$\frac{n（n-3）}{2}$，属于基础题，中考常考题型．
练习册系列答案
相关题目
17．春节前夕，某旅游景区的成人票和学生票均对折，李凯同学一家（2个成人和1个学生）去了该景区，门票共花费200元，王玲同学一家（3个成人和2个学生）去了该景区，门票共花费320元，则赵芸同学和妈妈去该景区游玩时，门票需要花费（ ）
| A． | 120元 | B． | 130元 | C． | 140元 | D． | 150元 |
14．
如图，两个天平都平衡，则与2个球体相等质量的正方体的个数为（ ）
如图，两个天平都平衡，则与2个球体相等质量的正方体的个数为（ ）| A． | 2 | B． | 3 | C． | 4 | D． | 5 |
1．
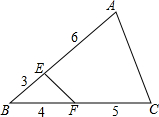如图，三角形ABC被分成三角形BEF和四边形AEFC两部分，BE=3，BF=4，FC=5，AE=6，那么三角形BEF面积和四边形AEFC面积的比是（ ）
如图，三角形ABC被分成三角形BEF和四边形AEFC两部分，BE=3，BF=4，FC=5，AE=6，那么三角形BEF面积和四边形AEFC面积的比是（ ）| A． | 4：23 | B． | 4：25 | C． | 5：26 | D． | 1：6 |
11．下列从左边到右边的变形，因式分解正确的是（ ）
| A． | 2a2-2=2（a+1）（a-1） | B． | （a+3）（a-3）=a2-9 | ||
| C． | -ab2+2ab-3b=-b（ab-2a-3） | D． | x2-2x-3=x（x-2）-3 |
18．$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{3}}$+$\frac{1}{{2}^{4}}$+…+$\frac{1}{{2}^{n}}$的值为（ ）
| A． | 1 | B． | $\frac{{2}^{n-2}}{{2}^{n}}$ | C． | 1-$\frac{1}{{2}^{n}}$ | D． | $\frac{{2}^{n}-1}{2n}$ |
15．一个商人将99颗弹子放进两个盒子，每个大盒子装12个，每个小盒子装5个，恰好装完．盒子总个数大于9，问大小盒子各几个？（ ）
| A． | 大的2个，小的15个 | |
| B． | 大的7个，小的3个 | |
| C． | 大的2个，小的15个或 大的7个，小的3个 | |
| D． | 无数种 |
16．三角形两边的长分别是8和6，第三边的长是一元二次方程x2-16x+60=0的一个实数根，则该三角形的面积是
（ ）
（ ）
| A． | 24 | B． | 24或8$\sqrt{5}$ | C． | 48或16$\sqrt{5}$ | D． | 8$\sqrt{5}$ |