题目内容
11．
如图，在平面直角坐标系中，点P为（-2，3），以点O为圆心，以OP的长为半径画弧，交x轴的负半轴于点A，则点A的横坐标介于（ ）| A． | -2.5和-3之间 | B． | -3和-3.5之间 | C． | -3.5和-4之间 | D． | -4和-4.5 之间 |
分析 先根据勾股定理求出OP的长，由于OP=OA，故估算出OP的长，再根据点A在x轴的负半轴上即可得出结论．
解答 解：∵点P坐标为（-2，3），
∴OP=$\sqrt{（-2）^{2}+{3}^{2}}$=$\sqrt{13}$，
∵点A、P均在以点O为圆心，以OP为半径的圆上，
∴OA=OP=$\sqrt{13}$，
∵12.25＜13＜16，
∴3.5＜$\sqrt{13}$＜4．
∵点A在x轴的负半轴上，
∴点A的横坐标介于-4和-3.5之间．
故选C．
点评 本题考查的是勾股定理及估算无理数的大小，根据题意利用勾股定理求出OP的长是解答此题的关键．
练习册系列答案
相关题目
1．
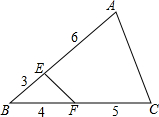如图，三角形ABC被分成三角形BEF和四边形AEFC两部分，BE=3，BF=4，FC=5，AE=6，那么三角形BEF面积和四边形AEFC面积的比是（ ）
如图，三角形ABC被分成三角形BEF和四边形AEFC两部分，BE=3，BF=4，FC=5，AE=6，那么三角形BEF面积和四边形AEFC面积的比是（ ）| A． | 4：23 | B． | 4：25 | C． | 5：26 | D． | 1：6 |
2．x是不大于5的正数，则下列表示正确的是（ ）
| A． | 0＜x＜5 | B． | 0＜x≤5 | C． | 0≤x≤5 | D． | x≤5 |
16．三角形两边的长分别是8和6，第三边的长是一元二次方程x2-16x+60=0的一个实数根，则该三角形的面积是
（ ）
（ ）
| A． | 24 | B． | 24或8$\sqrt{5}$ | C． | 48或16$\sqrt{5}$ | D． | 8$\sqrt{5}$ |
如图，点P在∠AOB内，点M，N分别是点P关于AO，BO的对称点，若△PEF的周长等于20cm，则MN的长为20cm．
20．
如图，在△ABC中，直线MN为BC的垂直平分线，交BC于点E，点D在直线MN上，且在△ABC的外面，连接BD，CD，若CA平分∠BCD，∠A=65°，∠ABC=85°，则△BCD是（ ）
如图，在△ABC中，直线MN为BC的垂直平分线，交BC于点E，点D在直线MN上，且在△ABC的外面，连接BD，CD，若CA平分∠BCD，∠A=65°，∠ABC=85°，则△BCD是（ ）| A． | 等边三角形 | B． | 等腰三角形 | C． | 直角三角形 | D． | 等腰直角三角形 |
