题目内容
10.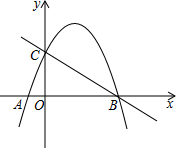 如图,在平面直角坐标系中,抛物线y=-$\frac{3}{4}$x2+bx+c与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,直线y=-$\frac{3}{4}$x+3经过B,C两点.
如图,在平面直角坐标系中,抛物线y=-$\frac{3}{4}$x2+bx+c与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,直线y=-$\frac{3}{4}$x+3经过B,C两点.(1)求抛物线的解析式;
(2)点P为直线BC上方抛物线上的一个动点,且点P的横坐标为a,如果S△PCB=2,求a的值;
(3)若点M为抛物线y=-$\frac{3}{4}$x2+bx+c上的一个动点,在直线BC上是否存在一点N,使得以M,N,C,O为顶点且以OC为边的四边形是平行四边形?若存在,请求出点N的坐标,若不存在,请说明理由.
分析 (1)首先求出B、C两点坐标,再利用待定系数法即可解决问题;
(2)如图设P(a,-$\frac{3}{4}$a2+$\frac{9}{4}$a+3),由S△PBC=2,推出S△POC+S△POB-S△OBC=2,可得$\frac{1}{2}$•3•a+$\frac{1}{2}$•4•(-$\frac{3}{4}$a2+$\frac{9}{4}$a+3)-$\frac{1}{2}$•4•3=2解方程即可解决问题;
(3)由题意当MN=OC,且MN∥OC时,以M,N,C,O为顶点且以OC为边的四边形是平行四边形,设N(m,-$\frac{3}{4}$m+3),则M(m,-$\frac{3}{4}$m2+$\frac{9}{4}$m+3),由题意当MN=OC时,
则有|-$\frac{3}{4}$m+3-(-$\frac{3}{4}$m2+$\frac{9}{4}$m+3)|=3,解方程即可;
解答 解:(1)由题意C(0,3),B(4,0),
把C(0,3),B(4,0)代入y=-$\frac{3}{4}$x2+bx+c,
得到$\left\{\begin{array}{l}{c=3}\\{-12+4b+c=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{b=\frac{9}{4}}\\{c=3}\end{array}\right.$,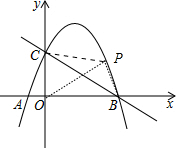
∴抛物线的解析式为y=-$\frac{3}{4}$x2+$\frac{9}{4}$x+3.
(2)如图设P(a,-$\frac{3}{4}$a2+$\frac{9}{4}$a+3),
∵S△PBC=2,
∴S△POC+S△POB-S△OBC=2,
∴$\frac{1}{2}$•3•a+$\frac{1}{2}$•4•(-$\frac{3}{4}$a2+$\frac{9}{4}$a+3)-$\frac{1}{2}$•4•3=2,
解得a=$\frac{6±2\sqrt{6}}{3}$.
(3)由题意当MN=OC,且MN∥OC时,以M,N,C,O为顶点且以OC为边的四边形是平行四边形,
设N(m,-$\frac{3}{4}$m+3),则M(m,-$\frac{3}{4}$m2+$\frac{9}{4}$m+3),由题意当MN=OC时,
则有|-$\frac{3}{4}$m+3-(-$\frac{3}{4}$m2+$\frac{9}{4}$m+3)|=3,
解得m=2或2+2$\sqrt{2}$或2-2$\sqrt{2}$,
∴满足条件的点M的坐标为2或2+2$\sqrt{2}$或2-2$\sqrt{2}$.
点评 本题考查二次函数综合题、待定系数法、三角形的面积、平行四边形的判定和性质等知识,解题的关键是学会用分割法求三角形的面积,学会用构建方程的思想思考问题,属于中考压轴题.

 阅读快车系列答案
阅读快车系列答案| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 无实数根 | D. | 无法确定根的情况 |
| A. | x+2y=1 | B. | 3x+2y=-8 | C. | 5x+4y=-3 | D. | 3x-4y=5 |
 如图,在一个边长为20cm的正方形的四角上,都剪去一个大小相同的小正方形,当小正方形的边长由小到大变化时,图中阴影部分的面积也随之发生变化.
如图,在一个边长为20cm的正方形的四角上,都剪去一个大小相同的小正方形,当小正方形的边长由小到大变化时,图中阴影部分的面积也随之发生变化.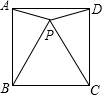 如图,正方形ABCD中有一点P,边长为4,且△PBC是等边三角形,则∠APD=150°,S△APB=4.
如图,正方形ABCD中有一点P,边长为4,且△PBC是等边三角形,则∠APD=150°,S△APB=4. 如图,在正方形ABCD中,点E是AD边上的一点,AF⊥BE于F,CG⊥BE于G.
如图,在正方形ABCD中,点E是AD边上的一点,AF⊥BE于F,CG⊥BE于G.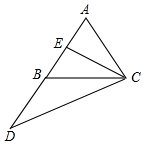 如图,在△ABC中,AB=AC,D是AB延长线上一点,BD=AB,E是AB的中点,求证:CE=$\frac{1}{2}$CD.
如图,在△ABC中,AB=AC,D是AB延长线上一点,BD=AB,E是AB的中点,求证:CE=$\frac{1}{2}$CD.