题目内容
20.已知 $\sqrt{\frac{x-6}{9-x}}$=$\frac{\sqrt{x-6}}{\sqrt{9-x}}$,且x为奇数,求(1+x)•$\sqrt{\frac{{x}^{2}-5x+4}{{x}^{2}-1}}$的值.分析 先根据二次根式的乘除法则求出x的值,再把原式进行化简,把x的值代入进行计算即可.
解答 解:∵$\sqrt{\frac{x-6}{9-x}}$=$\frac{\sqrt{x-6}}{\sqrt{9-x}}$,
∴$\left\{\begin{array}{l}x-6≥0\\ 9-x>0\end{array}$,
解得6≤x<9.
又∵x是奇数,∴x=7.
∴(1+x)•$\sqrt{\frac{{x}^{2}-5x+4}{{x}^{2}-1}}$
=(1+x)$\sqrt{\frac{(x-1)(x-4)}{(x+1)(x-1)}}$
=(1+x)$\sqrt{\frac{x-4}{x+1}}$
∴当x=7时,
原式=(1+7)$\sqrt{\frac{7-4}{7+1}}$
=2$\sqrt{6}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
12.若关于x的方程$\frac{a-2x}{x+2}$=1的解是负数,则a的取值范围是( )
| A. | a<2 | B. | a>2 | C. | a<2,且a≠-4 | D. | a>2,且a≠4 |
9.首都国际机场连续五年排名全球最繁忙机场第二位,该机场2012-2016年客流量统计结果如表:
根据统计表中提供的信息,预估首都国际机场2017年客流量约9823万人次,你的预估理由是由之前连续3年增长率预估2017年客流量的增长率约为4.5%.
| 年份 | 2012 | 2013 | 2014 | 2015 | 2016 |
| 客流量(万人次) | 8192 | 8371 | 8613 | 8994 | 9400 |
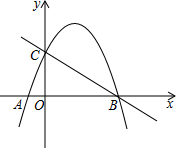 如图,在平面直角坐标系中,抛物线y=-$\frac{3}{4}$x2+bx+c与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,直线y=-$\frac{3}{4}$x+3经过B,C两点.
如图,在平面直角坐标系中,抛物线y=-$\frac{3}{4}$x2+bx+c与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,直线y=-$\frac{3}{4}$x+3经过B,C两点. 如图,AD=BD,AE=EC,延长DE到F,使EF=DE,连接AF、FC、CD,求证:四边形DBCF是平行四边形.
如图,AD=BD,AE=EC,延长DE到F,使EF=DE,连接AF、FC、CD,求证:四边形DBCF是平行四边形. 在直角坐标中反比例函数y=$\frac{6}{x}$的图象如图所示.
在直角坐标中反比例函数y=$\frac{6}{x}$的图象如图所示.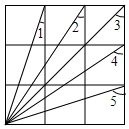 如图,在3×3的正方形网格中,则∠1+∠2+∠3+∠4+∠5等于225°.
如图,在3×3的正方形网格中,则∠1+∠2+∠3+∠4+∠5等于225°.