题目内容
13.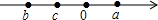 “数形结合”是一种重要的数字方法.如在化简|a|时,当a在数轴上位于原点的右侧时,|a|=a;当a在数轴上位于原点时,|a|=0;当a在数轴上位原点的左侧时,|a|=-a.试用这种方法解决下列问题.
“数形结合”是一种重要的数字方法.如在化简|a|时,当a在数轴上位于原点的右侧时,|a|=a;当a在数轴上位于原点时,|a|=0;当a在数轴上位原点的左侧时,|a|=-a.试用这种方法解决下列问题.(1)当a=1.5,b=-2.5时,$\frac{|a|}{a}-\frac{b}{|b|}$=2;
(2)请根据a、b、c三个数在数轴上的位置
①求$\frac{a}{|a|}$+$\frac{b}{|b|}$+$\frac{c}{|c|}$的值.
②化简:|a-b|-2|a+b|+|b+c|.
分析 (1)根据绝对值的性质,即可解答;
(2)①根据绝对值的性质,即可解答;
②根据数轴判定a-b、a+b、b+c的符号,即可解答.
解答 解:(1)∵a=1.5,b=-2.5,
∴a>0,b<0,
∴$\frac{|a|}{a}-\frac{b}{|b|}$=$\frac{a}{a}-\frac{b}{-b}$=1+1=2,
故答案为:2;
(2)①由数轴上a,b,c的位置可得:|a|=a,|b|=-b,|c|=-c,
故原式=$\frac{a}{a}+\frac{b}{-b}+\frac{c}{-c}$
=1-1-1
=-1.
②由数轴上a,b的位置可得:a-b>0,a+b<0,b+c<0,
故原式=a-b+(a+b)-(b+c)
=3a-c.
点评 本题考查了绝对值的性质,解决本题的关键是熟记绝对值的性质.

练习册系列答案
相关题目
4.若三角形的两边长分别为7和9,则第三边的长不可能是( )
| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
5.抛物线y=-3(x+2)2-4的开口方向和对称轴分别是( )
| A. | 向上,x=2 | B. | 向上,x=-2 | C. | 向下,x=2 | D. | 向下,x-=2 |
 如图,△AED∽△ABC,相似比为1:2.若BC=6,则DE的长是多少?
如图,△AED∽△ABC,相似比为1:2.若BC=6,则DE的长是多少?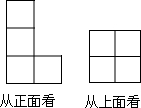 如图所示,是由若干个完全相同的小正方体搭成的几何体的从正面和从上面看到的形状图,则这个几何体可能是由6或7或8个小正方体搭成的.
如图所示,是由若干个完全相同的小正方体搭成的几何体的从正面和从上面看到的形状图,则这个几何体可能是由6或7或8个小正方体搭成的. 如图,点D为等腰直角三角形ABC内一点,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA.
如图,点D为等腰直角三角形ABC内一点,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA.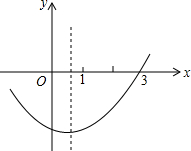 如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,现有下列结论:①abc<0;②b2-4ac+5>0;③2a+b<0;④a-b+c<0;⑤抛物线y=ax2+bx+c(a≠0)与x轴的另一个点坐标为(-1,0),其中正确的是②④(把所有正确结论的序号都填在横线上)
如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,现有下列结论:①abc<0;②b2-4ac+5>0;③2a+b<0;④a-b+c<0;⑤抛物线y=ax2+bx+c(a≠0)与x轴的另一个点坐标为(-1,0),其中正确的是②④(把所有正确结论的序号都填在横线上)