题目内容
2. 如图,点D为等腰直角三角形ABC内一点,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA.
如图,点D为等腰直角三角形ABC内一点,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA.(1)求∠EDC的度数;
(2)若点M在DE上,且DC=DM,求证:ME=BD.
分析 (1)证明△ACD≌△BCD即可解题;
(2)连接CM,先证明CM=CD,即可证明△BCD≌△ECM,即可解题.
解答 (1)解:∵AC=BC,∠CAD=∠CBD,
∴∠DAB=∠DBA,
∴AD=BD,
在△ACD和△BCD中,
$\left\{\begin{array}{l}{AD=BD}\\{∠CAD=∠CBD}\\{AC=BC}\end{array}\right.$,
∴△ACD≌△BCD(SAS),
∴∠ACD=∠BCD=45°,
∴∠CDE=∠CAD+∠ACD=60°;
(2)证明:连接CM,
∵DC=DM,∠CDE=60°,
∴△DMC为等边三角形,
∴∠MCE=45°,
∴CM=CD,
在△BCD和△ECM中,
$\left\{\begin{array}{l}{CD=CM}\\{∠BCD=∠ECM}\\{CB=CE}\end{array}\right.$,
∴△BCD≌△ECM(SAS),
∴ME=BD.
点评 本题考查了全等三角形的判定与性质,涉及等腰直角三角形,线段垂直平分线的判定与性质、等腰三角形的性质等知识点,难易程度适中,是一道很典型的题目.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
14.两个非零有理数的和为零,则它们的商是( )
| A. | -1 | B. | 0 | C. | 1 | D. | -1或1 |
11.一钝角三角形的钝角为120°,则其两锐角的角平分线相交所夹的钝角为( )
| A. | 120° | B. | 135° | C. | 145° | D. | 150° |
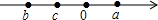 “数形结合”是一种重要的数字方法.如在化简|a|时,当a在数轴上位于原点的右侧时,|a|=a;当a在数轴上位于原点时,|a|=0;当a在数轴上位原点的左侧时,|a|=-a.试用这种方法解决下列问题.
“数形结合”是一种重要的数字方法.如在化简|a|时,当a在数轴上位于原点的右侧时,|a|=a;当a在数轴上位于原点时,|a|=0;当a在数轴上位原点的左侧时,|a|=-a.试用这种方法解决下列问题.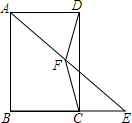 如图,在四边形ABCD中,AD∥BC,AD=BC,∠ABC=90°,点E在BC的延长线上,连接AE,点F为AE的中点.求证:DF=FC.
如图,在四边形ABCD中,AD∥BC,AD=BC,∠ABC=90°,点E在BC的延长线上,连接AE,点F为AE的中点.求证:DF=FC.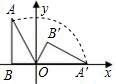 如图,在Rt△ABO中,∠B=90°,∠A=30°,OB=2,现将Rt△ABO在坐标平面内绕原点O按顺时针方向旋转到△OA′B′的位置.求:
如图,在Rt△ABO中,∠B=90°,∠A=30°,OB=2,现将Rt△ABO在坐标平面内绕原点O按顺时针方向旋转到△OA′B′的位置.求: