题目内容
20.若三角形三条边长分别为a,b,c,且a2b-a2c+b2c-b3=0,则这个三角形一定是等腰三角形.分析 首先需要将a2b-a2c+b2c-b3因式分解,则可得到(b-c)(a-b)(a+b)=0,即可得到:b=c或a=b,即这个三角形一定是等腰三角形.
解答 解:∵a2b-a2c+b2c-b3=a2(b-c)-b2(b-c)=(b-c)(a2-b2)=(b-c)(a-b)(a+b)=0,
∴b-c=o或a-b=0或a+b=0(舍去),
∴b=c或a=b.
∴这个三角形一定是等腰三角形.
故答案为:等腰三角形.
点评 此题考查了因式分解的应用.注意掌握因式分解的步骤,分解要彻底.

练习册系列答案
相关题目
11.已知点A、B分别在x轴正半轴、y轴正半轴上移动,AB=4,则以AB为直径的圆周所扫过的区域面积为( )
| A. | 4π | B. | 8π | C. | 2π+4 | D. | 6π+4 |
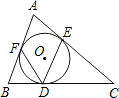 如图,△ABC的内切圆为⊙O,切点分别为D、E、F,若∠A=58°,求∠EDF的度数.
如图,△ABC的内切圆为⊙O,切点分别为D、E、F,若∠A=58°,求∠EDF的度数.
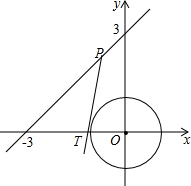 如图,在直角坐标系中,圆O是以坐标原点为圆心,半径为1的圆,直线L的方程为x-y+3=0,在L上任取一点P作圆O的切线,切点为T,则PT长的最小值是$\frac{\sqrt{14}}{2}$.
如图,在直角坐标系中,圆O是以坐标原点为圆心,半径为1的圆,直线L的方程为x-y+3=0,在L上任取一点P作圆O的切线,切点为T,则PT长的最小值是$\frac{\sqrt{14}}{2}$.