题目内容
13.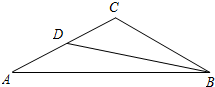 如图,已知在△ABC中,∠ABC=30°,BC=8,sin∠A=$\frac{{\sqrt{5}}}{5}$,BD是AC边上的中线.求:
如图,已知在△ABC中,∠ABC=30°,BC=8,sin∠A=$\frac{{\sqrt{5}}}{5}$,BD是AC边上的中线.求:(1)△ABC的面积;
(2)∠ABD的余切值.
分析 (1)过点C作CE⊥AB与点E,根据已知条件分别解△BCE、△ACE可得BE、CE、AE的长,即可计算S△ABC;
(2)过点D作DH⊥AB与点H知DH∥CE,由D是AC中点可得HE=$\frac{1}{2}$AE、DH=$\frac{1}{2}$CE,即可得cot∠ABD.
解答 解:(1)如图,过点C作CE⊥AB与点E,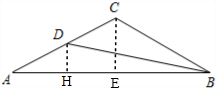
在RT△BCE中,∵BC=8,∠ABC=30°,
∴BE=BC•cos∠ABC=8×$\frac{\sqrt{3}}{2}$=4$\sqrt{3}$,
CE=BC•sin∠ABC=8×$\frac{1}{2}$=4,
在RT△ACE中,∵sin∠A=$\frac{{\sqrt{5}}}{5}$,
∴AC=$\frac{CE}{sin∠A}$=$\frac{4}{\frac{\sqrt{5}}{5}}$=4$\sqrt{5}$,
∴AE=$\sqrt{A{C}^{2}-C{E}^{2}}$=$\sqrt{(4\sqrt{5})^{2}-{4}^{2}}$=8,
则AB=AE+BE=8+4$\sqrt{3}$,
故S△ABC=$\frac{1}{2}$•AB•CE=$\frac{1}{2}$×(8+4$\sqrt{3}$)×4=16+8$\sqrt{3}$;
(2)过点D作DH⊥AB与点H,
∵CE⊥AB,
∴DH∥CE,
又∵D是AC中点,
∴AH=HE=$\frac{1}{2}$AE=4,DH=$\frac{1}{2}$CE=2,
∴在RT△BDH中,cot∠ABD=$\frac{BH}{DH}$=$\frac{4\sqrt{3}+4}{2}$=2$\sqrt{3}$+2.
点评 本题考查了解直角三角形、勾股定理、三角形中位线定理,通过作辅助线构造直角三角形是解题的关键.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案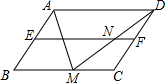 如图,在?ABCD中,AB=3,AD=5,AM平分∠BAD,交BC于点M,点E,F分别是AB,CD的中点,DM与EF交于点N,则NF的长等于( )
如图,在?ABCD中,AB=3,AD=5,AM平分∠BAD,交BC于点M,点E,F分别是AB,CD的中点,DM与EF交于点N,则NF的长等于( )| A. | 0.5 | B. | 1 | C. | $\sqrt{2}$ | D. | 2 |
 如图,l1∥l2∥l3,根据“平行线分线段成比例定理”,下列比例式中正确的是( )
如图,l1∥l2∥l3,根据“平行线分线段成比例定理”,下列比例式中正确的是( )| A. | $\frac{AD}{BC}=\frac{CE}{DF}$ | B. | $\frac{AD}{BE}=\frac{BC}{AF}$ | C. | $\frac{AB}{CD}=\frac{CD}{EF}$ | D. | $\frac{AD}{BC}=\frac{DF}{CE}$ |
 如图,排球在黑白两色的方砖上随机滚动,落在每块方砖上的可能性相同(若落在线上,则随机滚动一次).
如图,排球在黑白两色的方砖上随机滚动,落在每块方砖上的可能性相同(若落在线上,则随机滚动一次). 如图,在2×2的正方形网格中四个小正方形的顶点叫格点,已经取定格点A和B,在余下的格点中任取一点C,使△ABC为直角三角形的概率是$\frac{4}{7}$.
如图,在2×2的正方形网格中四个小正方形的顶点叫格点,已经取定格点A和B,在余下的格点中任取一点C,使△ABC为直角三角形的概率是$\frac{4}{7}$.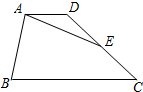 如图,已知在梯形ABCD中,AD∥BC,且BC=3AD,点E是边DC的中点.设$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AD}=\overrightarrow b$,那么$\overrightarrow{AE}$=$\frac{1}{2}$$\overrightarrow{a}$+2$\overrightarrow{b}$(用$\overrightarrow a$、$\overrightarrow b$的式子表示).
如图,已知在梯形ABCD中,AD∥BC,且BC=3AD,点E是边DC的中点.设$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AD}=\overrightarrow b$,那么$\overrightarrow{AE}$=$\frac{1}{2}$$\overrightarrow{a}$+2$\overrightarrow{b}$(用$\overrightarrow a$、$\overrightarrow b$的式子表示).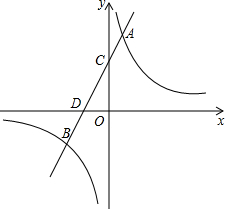 如图,直线y=mx+4与反比例函数y=$\frac{k}{x}$(k>0)的图象交于点A、B,与x轴、y轴分别交于D、C,tan∠CDO=2,AC:CD=1:2.
如图,直线y=mx+4与反比例函数y=$\frac{k}{x}$(k>0)的图象交于点A、B,与x轴、y轴分别交于D、C,tan∠CDO=2,AC:CD=1:2.