题目内容
3. 如图,排球在黑白两色的方砖上随机滚动,落在每块方砖上的可能性相同(若落在线上,则随机滚动一次).
如图,排球在黑白两色的方砖上随机滚动,落在每块方砖上的可能性相同(若落在线上,则随机滚动一次).(1)滚动一次,排球恰好落在白色方砖上的概率是$\frac{1}{2}$;
(2)连续滚动两次,排球两次都恰好落在白色方砖上的概率是多少呢?请通过画树状图或列表的方法求出这个概率.
分析 (1)由共有4种等可能的结果,排球恰好落在白色方砖上的有2种情况,直接利用概率公式求解即可求得答案;
(2)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与排球两次都恰好落在白色方砖上的情况,再利用概率公式即可求得答案.
解答 解:(1)∵共有4种等可能的结果,排球恰好落在白色方砖上的有2种情况,
∴滚动一次,排球恰好落在白色方砖上的概率是:$\frac{2}{4}$=$\frac{1}{2}$;
故答案为:$\frac{1}{2}$;
(2)画树状图得:
∵共有16种等可能的结果,排球两次都恰好落在白色方砖上的有4种情况,
∴排球两次都恰好落在白色方砖上的概率为:$\frac{4}{16}$=$\frac{1}{4}$.
点评 此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.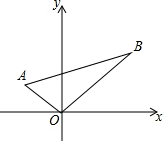 如图,在平面直角坐标系中,Rt△AOB的直角顶点与原点O重合,顶点A的坐标为(-1,1),∠ABO=30°,若顶点B在第一象限,则点B的坐标为( )
如图,在平面直角坐标系中,Rt△AOB的直角顶点与原点O重合,顶点A的坐标为(-1,1),∠ABO=30°,若顶点B在第一象限,则点B的坐标为( )
 如图,在平面直角坐标系中,Rt△AOB的直角顶点与原点O重合,顶点A的坐标为(-1,1),∠ABO=30°,若顶点B在第一象限,则点B的坐标为( )
如图,在平面直角坐标系中,Rt△AOB的直角顶点与原点O重合,顶点A的坐标为(-1,1),∠ABO=30°,若顶点B在第一象限,则点B的坐标为( )| A. | (1,1) | B. | ($\sqrt{2}$,$\sqrt{2}$) | C. | ($\sqrt{3}$,$\sqrt{3}$) | D. | (2,2) |
18.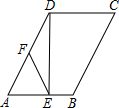 如图,在?ABCD中,∠A=65°,DE⊥AB,垂足为点E,点F为边AD上的中点,连接FE,则∠AFE的度数为( )
如图,在?ABCD中,∠A=65°,DE⊥AB,垂足为点E,点F为边AD上的中点,连接FE,则∠AFE的度数为( )
 如图,在?ABCD中,∠A=65°,DE⊥AB,垂足为点E,点F为边AD上的中点,连接FE,则∠AFE的度数为( )
如图,在?ABCD中,∠A=65°,DE⊥AB,垂足为点E,点F为边AD上的中点,连接FE,则∠AFE的度数为( )| A. | 40° | B. | 50° | C. | 60° | D. | 70° |
 如图,已知AD∥BE∥CF,$\frac{AB}{BC}=\frac{2}{3}$,DE=3,则DF的长为7.5.
如图,已知AD∥BE∥CF,$\frac{AB}{BC}=\frac{2}{3}$,DE=3,则DF的长为7.5.
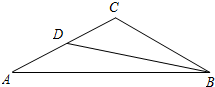 如图,已知在△ABC中,∠ABC=30°,BC=8,sin∠A=$\frac{{\sqrt{5}}}{5}$,BD是AC边上的中线.求:
如图,已知在△ABC中,∠ABC=30°,BC=8,sin∠A=$\frac{{\sqrt{5}}}{5}$,BD是AC边上的中线.求: