题目内容
7．
如图，网格中每个小正方形的边长均为1，线段AB，线段CD的端点均在小正方形的顶点上．（1）在图中画以AB为斜边的等腰直角△ABE，顶点E在小正方形的顶点上；
（2）在（1）的条件下，在图中以CD为边画直角△CDF，点F在小正方形的顶点上，使∠CDF=90°，且△CDF的面积为6，连接EF，直接写出EF的长．
分析 （1）以AB为斜边画出等腰直角三角形△ABE即可；
（2）根据要求画出△CDF即可，利用勾股定理求出EF的长；
解答 解：（1）等腰直角△ABE如图所示；
（2）△CDF如图所示，
EF=$\sqrt{{4}^{2}+{1}^{2}}$=$\sqrt{17}$．
点评 本题考查作图-应用与设计，勾股定理等知识，解题的关键是灵活运用所学知识解决问题，体现了数形结合的思想．
练习册系列答案
阅读快车系列答案
相关题目
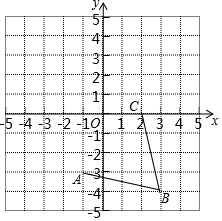如图，在平面直角坐标系中，网格中每一个小正方形的边长为1个单位长度，且点A、B、C均在格点上．
如图，△OAB的OA边在x轴上，其中B点坐标为（3，4）且OB=BA．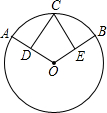
如图，在⊙O中，$\widehat{AC}$=$\widehat{CB}$，CD⊥OA于D，CE⊥OB于E，求证：AD=BE．