题目内容
12.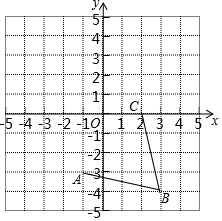 如图,在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度,且点A、B、C均在格点上.
如图,在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度,且点A、B、C均在格点上.(1)请在所给的网格内画出以线段AB、BC为边的菱形并写出点D的坐标(-2,1);
(2)菱形ABCD的周长为4$\sqrt{17}$;
(3)菱形ABCD的面积为15.
分析 (1)根据菱形的边长为$\sqrt{17}$,画出图形即可;
(2)利用勾股定理即可即可解决问题;
(3)求出菱形的对角线的长即可解决问题;
解答 解:(1)以线段AB、BC为边的菱形ABCD是菱形.D(-2,1).
故答案为D(-2,1).
(2)∵B(3,-4),C(2,0),
∴BC=$\sqrt{{4}^{2}+{1}^{2}}$=$\sqrt{17}$,
∴菱形ABCD的周长为4$\sqrt{17}$.
故答案为4$\sqrt{17}$.
(3)∵A(-1,-3),C(2,0),B(3,-4),D(-2,1),
∴AC=3$\sqrt{2}$,BD=5$\sqrt{2}$,
∴S菱形ABCD=$\frac{1}{2}$$•3\sqrt{2}$•5$\sqrt{2}$=15.
故答案为15.
点评 本题考查作图-应用与设计、勾股定理、菱形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
相关题目
10. 在长方形ABCD中,放入6个长度相同的小长方形,所标尺寸如图所示,设小长方形的宽AE=xcm,依题意可列方程( )
在长方形ABCD中,放入6个长度相同的小长方形,所标尺寸如图所示,设小长方形的宽AE=xcm,依题意可列方程( )
 在长方形ABCD中,放入6个长度相同的小长方形,所标尺寸如图所示,设小长方形的宽AE=xcm,依题意可列方程( )
在长方形ABCD中,放入6个长度相同的小长方形,所标尺寸如图所示,设小长方形的宽AE=xcm,依题意可列方程( )| A. | 6+2x=14-3x | B. | 6+2x=x+(14-3x) | C. | 6+2x=14-x | D. | 14-3x=6+2x |
20.已知a,b满足5a-5b+2ab=0,且ab≠0,则$\frac{1}{a}$-$\frac{1}{b}$的值是( )
| A. | 5 | B. | 2 | C. | $\frac{2}{5}$ | D. | $\frac{5}{2}$ |
4.若抛物线y=-x2+bx+c经过点(-2,3),则2c-4b-9的值是( )
| A. | 5 | B. | -1 | C. | 4 | D. | 18 |
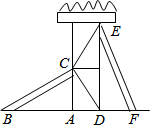 如图所示,有两个长度相同的滑梯BC和EF,CA⊥BF,ED⊥BF,垂足分别为A,D,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等.问:两个滑梯的倾斜角∠ABC和∠DFE的大小有什么关系?
如图所示,有两个长度相同的滑梯BC和EF,CA⊥BF,ED⊥BF,垂足分别为A,D,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等.问:两个滑梯的倾斜角∠ABC和∠DFE的大小有什么关系? 如图,网格中每个小正方形的边长均为1,线段AB,线段CD的端点均在小正方形的顶点上.
如图,网格中每个小正方形的边长均为1,线段AB,线段CD的端点均在小正方形的顶点上. 如图所示,在平面直角坐标系xOy中,A(-1,5),B(-1,0),C(-4,3),直线m为横坐标都为2的点组成的一条直线,作出△ABC关于直线m对称的△A1B1C1,并直接写出A1,B1,C1的坐标.
如图所示,在平面直角坐标系xOy中,A(-1,5),B(-1,0),C(-4,3),直线m为横坐标都为2的点组成的一条直线,作出△ABC关于直线m对称的△A1B1C1,并直接写出A1,B1,C1的坐标. 如图,直线AB⊥CD,垂足为O,直线EF经过点O,∠1=30°,求∠AOF、∠AOE和∠DOE的度数.
如图,直线AB⊥CD,垂足为O,直线EF经过点O,∠1=30°,求∠AOF、∠AOE和∠DOE的度数.