题目内容
6.已知x=2是关于x的一元二次方程x2+ax+b=0的一个根,则代数式a2+$\frac{1}{4}$b2+ab的值是4.分析 先根据一元二次方程的解的定义得到2a+b=0,即2a+b=-4,再利用配方法得到a2+$\frac{1}{4}$b2+ab=$\frac{1}{4}$×(2a+b)2,然后利用整体代入的方法计算.
解答 解:∵x=2是关于x的一元二次方程x2+ax+b=0的一个根,
∴4+2a+b=0,
即2a+b=-4,
∴a2+$\frac{1}{4}$b2+ab=$\frac{1}{4}$(4a2+4ab+b2)=$\frac{1}{4}$×(2a+b)2=$\frac{1}{4}$×(-4)2=4.
故答案是:4.
点评 本题考查了一元二次方程的解:能使一元二次方程左右两边相等的未知数的值是一元二次方程的解.

练习册系列答案
相关题目
17.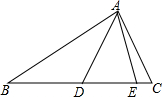 如图,在△ADE中,线段AE,AD的中垂线分别交直线DE于B和C两点,∠B=α,∠C=β,则∠DAE的度数分别为( )
如图,在△ADE中,线段AE,AD的中垂线分别交直线DE于B和C两点,∠B=α,∠C=β,则∠DAE的度数分别为( )
 如图,在△ADE中,线段AE,AD的中垂线分别交直线DE于B和C两点,∠B=α,∠C=β,则∠DAE的度数分别为( )
如图,在△ADE中,线段AE,AD的中垂线分别交直线DE于B和C两点,∠B=α,∠C=β,则∠DAE的度数分别为( )| A. | $\frac{α+β}{2}$ | B. | $\frac{β-α}{2}$ | C. | $\frac{180°-(α+β)}{2}$ | D. | $\frac{180°-(β-α)}{2}$ |
8.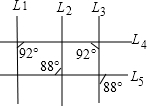 如图为平面上五条直线L1,L2,L3,L4,L5相交的情形,根据图中标示的角度,判断下列叙述何者正确( )
如图为平面上五条直线L1,L2,L3,L4,L5相交的情形,根据图中标示的角度,判断下列叙述何者正确( )
 如图为平面上五条直线L1,L2,L3,L4,L5相交的情形,根据图中标示的角度,判断下列叙述何者正确( )
如图为平面上五条直线L1,L2,L3,L4,L5相交的情形,根据图中标示的角度,判断下列叙述何者正确( )| A. | L1和L3平行,L2和L3平行 | B. | L1和L3平行,L2和L3不平行 | ||
| C. | L1和L3不平行,L2和L3平行 | D. | L1和L3不平行,L2和L3不平行 |
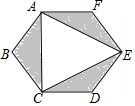 如图,正六边形ABCDEF是一块绿化带,阴影部分都是花圃,一只自由飞翔的小鸟,将随机落在这块绿化带上,则小鸟在花圃上的概率为$\frac{1}{2}$.
如图,正六边形ABCDEF是一块绿化带,阴影部分都是花圃,一只自由飞翔的小鸟,将随机落在这块绿化带上,则小鸟在花圃上的概率为$\frac{1}{2}$.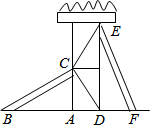 如图所示,有两个长度相同的滑梯BC和EF,CA⊥BF,ED⊥BF,垂足分别为A,D,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等.问:两个滑梯的倾斜角∠ABC和∠DFE的大小有什么关系?
如图所示,有两个长度相同的滑梯BC和EF,CA⊥BF,ED⊥BF,垂足分别为A,D,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等.问:两个滑梯的倾斜角∠ABC和∠DFE的大小有什么关系? 如图,网格中每个小正方形的边长均为1,线段AB,线段CD的端点均在小正方形的顶点上.
如图,网格中每个小正方形的边长均为1,线段AB,线段CD的端点均在小正方形的顶点上.