题目内容
19. 如图,△OAB的OA边在x轴上,其中B点坐标为(3,4)且OB=BA.
如图,△OAB的OA边在x轴上,其中B点坐标为(3,4)且OB=BA.(1)求经过A,B,O三点的抛物线的解析式;
(2)将(1)中的抛物线沿x轴平移,设点A,B的对应点分别为点A′,B′,若四边形ABB′A′为菱形,求平移后的抛物线的解析式.
分析 (1)设所求抛物线的解析式为y=ax(x-6),将(3,4)代入即可得到结论;
(2)根据勾股定理得到BA=$\sqrt{{3}^{2}+{4}^{2}}$=5,根据菱形的性质得到BB′=BA=5,①若抛物线沿x轴向右平移,求得B′(8,4),于是得到平移后抛物线的解析式为y=-$\frac{4}{9}$(x-8)2+4;②若抛物线沿x轴向左平移,得到B′(-2,4),于是得到平移后抛物线的解析式为y=-$\frac{4}{9}$(x+2)2+4.
解答 解:(1)∵B点坐标为(3,4)且OB=BA,
∴A(6,0),
设所求抛物线的解析式为y=ax(x-6),将(3,4)代入,可得4=-9a,
∴a=-$\frac{4}{9}$,
∴y=-$\frac{4}{9}$x(x-6)=-$\frac{4}{9}$x2+$\frac{8}{3}$x;
(2)∵B点坐标为(3,4),OB=BA,
∴A(6,0),
∴BA=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∵四边形ABB′A′为菱形,
∴BB′=BA=5,
①若抛物线沿x轴向右平移,则B′(8,4),
∴平移后抛物线的解析式为y=-$\frac{4}{9}$(x-8)2+4;
②若抛物线沿x轴向左平移,则B′(-2,4),∴平移后抛物线的解析式为y=-$\frac{4}{9}$(x+2)2+4.
点评 本题考查了二次函数的图象与几何变换,菱形的性质,等腰三角形的性质,待定系数法求函数的解析式,正确的理解题意是解题的关键.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
17.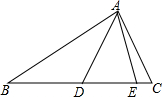 如图,在△ADE中,线段AE,AD的中垂线分别交直线DE于B和C两点,∠B=α,∠C=β,则∠DAE的度数分别为( )
如图,在△ADE中,线段AE,AD的中垂线分别交直线DE于B和C两点,∠B=α,∠C=β,则∠DAE的度数分别为( )
 如图,在△ADE中,线段AE,AD的中垂线分别交直线DE于B和C两点,∠B=α,∠C=β,则∠DAE的度数分别为( )
如图,在△ADE中,线段AE,AD的中垂线分别交直线DE于B和C两点,∠B=α,∠C=β,则∠DAE的度数分别为( )| A. | $\frac{α+β}{2}$ | B. | $\frac{β-α}{2}$ | C. | $\frac{180°-(α+β)}{2}$ | D. | $\frac{180°-(β-α)}{2}$ |
14. 一个有进水管和出水管的容器,从某时刻开始4min内只进水不出水,在随后的8min内既进水又出水,每分钟的进水量和出水量是两个常数,容器内的水量y(L)与时间x(min)之间的关系如图所示,则每分钟的出水量为( )
一个有进水管和出水管的容器,从某时刻开始4min内只进水不出水,在随后的8min内既进水又出水,每分钟的进水量和出水量是两个常数,容器内的水量y(L)与时间x(min)之间的关系如图所示,则每分钟的出水量为( )
 一个有进水管和出水管的容器,从某时刻开始4min内只进水不出水,在随后的8min内既进水又出水,每分钟的进水量和出水量是两个常数,容器内的水量y(L)与时间x(min)之间的关系如图所示,则每分钟的出水量为( )
一个有进水管和出水管的容器,从某时刻开始4min内只进水不出水,在随后的8min内既进水又出水,每分钟的进水量和出水量是两个常数,容器内的水量y(L)与时间x(min)之间的关系如图所示,则每分钟的出水量为( )| A. | 5L | B. | 3.75L | C. | 2.5L | D. | 1.25L |
4.若抛物线y=-x2+bx+c经过点(-2,3),则2c-4b-9的值是( )
| A. | 5 | B. | -1 | C. | 4 | D. | 18 |
8.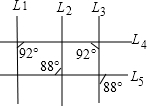 如图为平面上五条直线L1,L2,L3,L4,L5相交的情形,根据图中标示的角度,判断下列叙述何者正确( )
如图为平面上五条直线L1,L2,L3,L4,L5相交的情形,根据图中标示的角度,判断下列叙述何者正确( )
 如图为平面上五条直线L1,L2,L3,L4,L5相交的情形,根据图中标示的角度,判断下列叙述何者正确( )
如图为平面上五条直线L1,L2,L3,L4,L5相交的情形,根据图中标示的角度,判断下列叙述何者正确( )| A. | L1和L3平行,L2和L3平行 | B. | L1和L3平行,L2和L3不平行 | ||
| C. | L1和L3不平行,L2和L3平行 | D. | L1和L3不平行,L2和L3不平行 |
 如图,网格中每个小正方形的边长均为1,线段AB,线段CD的端点均在小正方形的顶点上.
如图,网格中每个小正方形的边长均为1,线段AB,线段CD的端点均在小正方形的顶点上.