Question

2．（1）【操作】在同一平面直角坐标系中，画出下列函数的图象：
①y=x+1；②y=x-1；③y=x-2．
并判断出这三个函数图象之间的位置关系．
（2）【猜想】已知直线y₁=k₁x+b₁和直线y₂=k₂x+b₂，由操作的结果可猜想：当k₁，k₂，b₁，b₂满足怎样的关系时，直线y₁=k₁x+b₁与直线y₂=k₂x+b₂之间相互平行（不用说理）．
（3）【应用】已知直线l与直线y=-2x平行，且经过点（-2，-3），试确定直线l的函数解析式．

Answer 1

分析 （1）根据一次函数的图象是直线，只需确定直线上两个特殊点即可；
（2）观察（1）的结果，归纳总结即可；
（3）利用（2）的结论，设直线l的函数解析式为y=-2x+b，将（-2，3）代入求得b，可得解析式．

解答 解：（1）函数y=x+1经过点（0，1），（-1，0），函数y=x-1经过点（0，-1），（1，0），函数y=x-2经过点（0，-2），（-2，0），
它们的图象如图所示：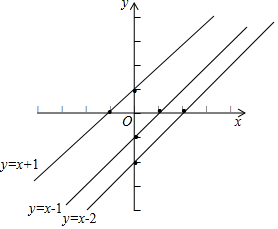

观察发现，三个函数图象相互平行；

（2）由（1）的图象知，
当k₁=k₂，b₁≠b₂时，直线y₁=k₁x+b₁与直线y₂=k₂x+b₂之间相互平行；

（3）设直线l的函数解析式为y=-2x+b，将（-2，3）代入得，
3=-2×（-2）+b，
解得，b=-1，
∴直线l的函数解析式为：y=-2x-1．

点评 本题主要考查了两直线平行和相交的问题，解题的关键是一次函数的图象是直线，确定两点即可画出直线．