题目内容
3.如图,直线y=2x-a(a<0)与y轴交于点A,与x轴交于点E,抛物线y=x2-2x+a的顶点为C,与y轴交于点B,直线BC与直线AE交于点D.
(1)求点B、C、D的坐标(用含a的代数式表示);
(2)抛物线上是否存在一点P,使得以P、A、B、D为顶点的四边形是平行四边形?若存在,求出a的值及此时点P的坐标;若不存在,请说明理由.
分析 (1)把x=0代入到y=x2-2x+a求点B的坐标,将二次函数的解析式配方可求C的坐标,求直线BC的解析式,再求直线BC和直线AE的交点D;
(2)存在,分两种情况:①以AB为对角线时,如图1,根据OD=OP确定P的坐标后代入抛物线的解析式中,求a的值,计算点P的坐标;
②以AB为边时,如图2,根据PD=AB列式得出结论.
解答 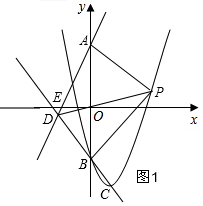 解:(1)当x=0时,y=a,
解:(1)当x=0时,y=a,
∴B(0,a),
y=x2-2x+a=(x-1)2+a-1,
∴顶点C(1,a-1),
设直线BC的解析式为:y=kx+b,
把B(0,a)、C(1,a-1)代入得:$\left\{\begin{array}{l}{b=a}\\{k+b=a-1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-1}\\{b=a}\end{array}\right.$,
∴直线BC的解析式为:y=-x+a,
则$\left\{\begin{array}{l}{y=-x+a}\\{y=2x-a}\end{array}\right.$ 解得:$\left\{\begin{array}{l}{x=\frac{2a}{3}}\\{y=\frac{a}{3}}\end{array}\right.$,
∴D($\frac{2a}{3}$,$\frac{a}{3}$);
(2)存在一点P,使得以P、A、B、D为顶点的四边形是平行四边形,
分两种情况:
①以AB为对角线时,如图1,
∵A(0,-a),B(0,a),
∴OA=OB,
∴O是?ADBP对角线的交点,
∴OD=OP,
∵D($\frac{2a}{3}$,$\frac{a}{3}$),
∴P(-$\frac{2a}{3}$,-$\frac{a}{3}$),
∵P在抛物线上,
∴-$\frac{a}{3}$=$(-\frac{2a}{3})^{2}$-2×$(-\frac{2a}{3})$+a,
解得:a=-6,
当a=-6时,-$\frac{2a}{3}$=-$\frac{2×(-6)}{3}$=4,
-$\frac{a}{3}$=-$\frac{-6}{3}$=2,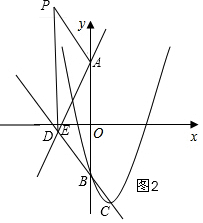
∴P(4,2);
②以AB为边时,如图2,
∵四边形ADBP是平行四边形,
∴AB=PD=-2a,AB∥PD,
∵AB⊥x轴,
∴PD⊥x轴,
∵D($\frac{2a}{3}$,$\frac{a}{3}$),
∴P($\frac{2a}{3}$,-$\frac{5a}{3}$),
∴-$\frac{5a}{3}$=$(\frac{2a}{3})^{2}-2×\frac{2a}{3}$+a,
a=-3,
当a=-3时,$\frac{2a}{3}$=$\frac{2×(-3)}{3}$=-2,
-$\frac{5a}{3}$=-$\frac{5×(-6)}{3}$=10,
∴P(-2,10);
综上所述,使得以P、A、B、D为顶点的四边形是平行四边形,此时点P(4,2)或(-2,10),对应a的值分别为-6或-3.
点评 此题主要考查了二次函数的综合应用,二次函数的综合应用是初中阶段的重点题型,特别注意利用数形结合是这部分考查的重点,也是难点,同时对于第2问构成平行四边形时,要采用分类讨论的思想解决.

 阅读快车系列答案
阅读快车系列答案 如图,在平面直角坐标系中,抛物线W的解斩式为y=-$\frac{1}{2}$x2-x+4,抛物线W与x轴交于A,B两点(点B在A的右侧),与y轴交于点C,一次函数y=kx+b的图象经过点B并且与y轴交于点D(0,3),与抛物线的另一个交点为E.
如图,在平面直角坐标系中,抛物线W的解斩式为y=-$\frac{1}{2}$x2-x+4,抛物线W与x轴交于A,B两点(点B在A的右侧),与y轴交于点C,一次函数y=kx+b的图象经过点B并且与y轴交于点D(0,3),与抛物线的另一个交点为E.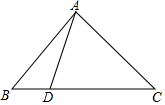 在△ABC中,∠A=90°,AB=AC,D为BC边上一点,求证:BD2+CD2=2AD2.
在△ABC中,∠A=90°,AB=AC,D为BC边上一点,求证:BD2+CD2=2AD2.