Question

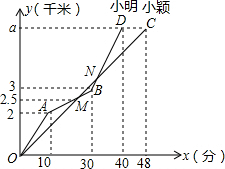为参加某市冬季越野赛，小明、小强两名同学进行了a千米的越野跑训练，在越野跑训练中的路程y（千米）与时间x（分）函数关系如图所示．
（1）根据图象提供的数据，求越野跑开始后，两人第一次相遇所用的时间；
（2）求两人第二次相遇时，离终点的距离．

Answer 1

考点：一次函数的应用

专题：

分析：（1）先由待定系数法求出AB的解析式，当y=2.5时代入解析式求出其解即可；
（2）由（2）的结论求出M的坐标，进而求出OC的解析式，当x=48时代入解析式求出a的值就可以求出D的坐标，由待定系数法求出BD的解析式，由一次函数与二元一次方程组的关系建立方程组求出其解即可．

解答：解：（1）设AB的解析式为y=kxb，由题意，得

2=10k+b 3=30k+b

，
解得：

k= 1 20 b= 3 2

．
则y=

1

20

x+

3

2

，
当y=2.5时，2.5=

1

20

x+

3

2

，
x=20．
则两人第一次相遇所用的时间为20分钟；
（2）由y=2.5时，x=20，
则M（20，2.5）．
设OC的解析式为y=k₁x，由题意，得
2.5=20k₁，
解得：k₁=

1

8

，
则y=

1

8

x．
当x=48时，y=6，
∴a=6．
∴D（40，6）．
设BD的解析式为y=mx+n，由题意，得

3=30m+n 6=40m+n

，
解得：

m=0.3 n=-6

，
∴y=0.3x-6，
∴

y= 1 8 x y=0.3x-6

，
解得：

x= 240 7 y= 30 7

．
∴离终点的距离为6-

30

7

=

12

7

千米．
答：两人第二次相遇时，离终点的距离为

12

7

千米．

点评：本题考查了行程问题的数量关系路程=速度×时间的运用，一次函数与二元一次方程组的关系的运用，待定系数法求一次函数的解析式的运用，解答时求出函数的解析式是关键．