题目内容
1.等腰直角△ABC中,∠BAC=90°,BC=8,⊙O过点B,C,点O在△ABC的外部,且OA=1,则⊙O的半径为( )| A. | 4 | B. | 5 | C. | $\sqrt{41}$ | D. | $4\sqrt{2}$ |
分析 根据题意首先作图并连接OC、OB,延长OA交BC于点D,交⊙O于点E,然后证明△OBD为直角三角形,利用已知条件及勾股定理即可求解
解答 解:如下图所示:连接OC、OB,延长OA交BC于点D,交⊙O于点E 
∵在△OAB与△OAC中,$\left\{\begin{array}{l}{OB=OC}\\{AB=AC}\\{OA=OA}\end{array}\right.$
∴△OAB≌△OAC,
∴∠OAB=∠OAC,
∴∠BAD=∠CAD
又∵AB=AC,
∴∠ADB=∠ADC=90°,BD=DC=AD=4
∴在Rt△ODB中,OB2=OD2+BD2,
∴OB2=52+42=41,
∴OB=$\sqrt{41}$
即:⊙O的半径是$\sqrt{41}$
点评 本题考查了圆与等腰直角三角形综合的有关问题,解题的关键是正确作图,并构建含半径及已知条件的直角三角形.

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
16.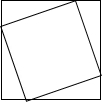 一个周长为20的正方形内接于一个周长为28的正方形,那么从里面正方形的顶点到外面正方形的顶点的最大距离是( )
一个周长为20的正方形内接于一个周长为28的正方形,那么从里面正方形的顶点到外面正方形的顶点的最大距离是( )
 一个周长为20的正方形内接于一个周长为28的正方形,那么从里面正方形的顶点到外面正方形的顶点的最大距离是( )
一个周长为20的正方形内接于一个周长为28的正方形,那么从里面正方形的顶点到外面正方形的顶点的最大距离是( )| A. | $\sqrt{58}$ | B. | $\frac{7}{2}$$\sqrt{5}$ | C. | 8 | D. | $\sqrt{65}$ | ||||
| E. | 5$\sqrt{3}$ |
10.下列说法正确的是( )
| A. | 同位角相等 | |
| B. | 和已知直线平行的直线有且只有一条 | |
| C. | 在平面内过一点有且只有一条直线垂直于已知直线 | |
| D. | 在平面内过一点有且只有一条直线平行于已知直线 |
11.已知四边形ABCD为任意凸四边形,E、F、G、H分别是边AB、BC、CD、DA的中点,用S、P分别表示四边形ABCD的面积和周长;S1、P1分别表示四边形EFGH的面积和周长.设K=$\frac{S}{{S}_{1}}$,K1=$\frac{P}{{P}_{1}}$,则下面关于K、K1的说法正确的是( )
| A. | K、K1均为常值 | B. | K为常值,K1不为常值 | ||
| C. | K不为常值,K1为常值 | D. | K、K1均不为常值 |
 的顶点都是正方形网格中的格点,则
的顶点都是正方形网格中的格点,则  等于( )
等于( ) 
 B.
B.  C.
C.  D.
D. 