题目内容
16.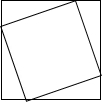 一个周长为20的正方形内接于一个周长为28的正方形,那么从里面正方形的顶点到外面正方形的顶点的最大距离是( )
一个周长为20的正方形内接于一个周长为28的正方形,那么从里面正方形的顶点到外面正方形的顶点的最大距离是( )| A. | $\sqrt{58}$ | B. | $\frac{7}{2}$$\sqrt{5}$ | C. | 8 | D. | $\sqrt{65}$ | ||||
| E. | 5$\sqrt{3}$ |
分析 设最大距离是x,已知大正方形和小正方形的周长,可得其边长,即可求出四个小三角形的面积,根据小三角形的面积列出一元二次方程,解得x的值即可判断正方形的一个顶点到外面的正方形的四个顶点的距离的最大值.
解答 解:如图所示:∵大正方形周长为28,
∴大正方形边长为7,
∵小正方形周长为20,
∴小正方形边长为5,
设最大距离是x,
则每个小三角形的面积是$\frac{7×7-5×5}{4}$=6,
$\frac{x(7-x)}{2}$=6,
x2-7x+12=0,
解得x=4或x=3,
故当AC=4,则AB=$\sqrt{{4}^{2}+{7}^{2}}$=$\sqrt{65}$,
所以从里面正方形的顶点到外面正方形的顶点的最大距离是$\sqrt{65}$.
故选:D.
点评 本题主要考查正方形的性质和勾股定理的知识点,解答本题的关键是求出每个小三角形的面积,熟练掌握解一元二次方程的方法,此题难度一般.

练习册系列答案
相关题目
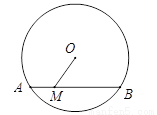
1.等腰直角△ABC中,∠BAC=90°,BC=8,⊙O过点B,C,点O在△ABC的外部,且OA=1,则⊙O的半径为( )
| A. | 4 | B. | 5 | C. | $\sqrt{41}$ | D. | $4\sqrt{2}$ |

 如图,在平面直角坐标系中,直线y=-$\frac{3}{4}$x+b分别与x轴、y轴交于点A、B,且点A的坐标为(8,0),点M是线段AB上的一个动点(点A、B除外),点N在x轴上方,使得以O、B、M、N为顶点的四边形是菱形,点N的坐标为($\frac{144}{25}$,$\frac{192}{25}$)或(-4,3).
如图,在平面直角坐标系中,直线y=-$\frac{3}{4}$x+b分别与x轴、y轴交于点A、B,且点A的坐标为(8,0),点M是线段AB上的一个动点(点A、B除外),点N在x轴上方,使得以O、B、M、N为顶点的四边形是菱形,点N的坐标为($\frac{144}{25}$,$\frac{192}{25}$)或(-4,3).