题目内容
10.抛物线y=ax2+2ax+c(a<0)向右平移2个单位后的新图上有两点A(x1,y1),B(x2,y2),在此函数图象上,如果x1<x2<0.则y1与y2的大小关系是y1<y2.分析 根据抛物线解析式求得对称轴x=-1,根据平移的规律得到平移后的抛物线对称轴是x=1.根据函数图象的增减性进行答题.
解答 解:∵抛物线y=ax2+2ax+c(a<0)的对称轴是x=-$\frac{2a}{2a}$=-1,
∴该抛物线向右平移2个单位后的对称轴为x=1.
又∵该抛物线的开口方向向下,
∴在x<1上,y随x的增大而增大,
∴当x1<x2<0,y1<y2的.
故答案是:y1<y2.
点评 本题考查了二次函数图象与几何变换.熟练掌握抛物线的增碱性是解题的突破口.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.若实数x,y满足|x-4|+$\sqrt{y-8}$=0,则以x,y的值为两边长的等腰三角形的周长是( )
| A. | 12 | B. | 16 | C. | 16或20 | D. | 20 |
15.在运动会上,成绩是按点到直线的距离来评定的有( )
| A. | 跳远 | B. | 跳高 | C. | 掷铅球 | D. | 掷标枪 |
2.某商场招募员工一名,现有甲、乙、丙三人竞聘.通过计算机技能、语言表达和商品知识三项测试,他们各自成绩(百分制)如下表:
(1)若商场需要招聘负责将商品拆装上架的人员,对计算机技能、语言表达和商品知识分别赋权2、3、5,计算这三名应试者的平均成绩.从成绩看,应该录取谁?
(2)若商场需要招聘电脑收银员,计算机技能、语言表达和商品知识成绩分别占50%、30%、20%,计算这三名应试者的平均成绩.从成绩看,应该录取谁?
| 应试者 | 计算机技能 | 语言表达 | 商品知识 |
| 甲 | 70 | 50 | 80 |
| 乙 | 90 | 75 | 45 |
| 丙 | 50 | 60 | 85 |
(2)若商场需要招聘电脑收银员,计算机技能、语言表达和商品知识成绩分别占50%、30%、20%,计算这三名应试者的平均成绩.从成绩看,应该录取谁?
20.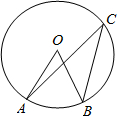 如图,点A、B、C都在⊙O上,⊙O的半径为2,∠ACB=30°,则$\widehat{AB}$的长是( )
如图,点A、B、C都在⊙O上,⊙O的半径为2,∠ACB=30°,则$\widehat{AB}$的长是( )
 如图,点A、B、C都在⊙O上,⊙O的半径为2,∠ACB=30°,则$\widehat{AB}$的长是( )
如图,点A、B、C都在⊙O上,⊙O的半径为2,∠ACB=30°,则$\widehat{AB}$的长是( )| A. | 2π | B. | π | C. | $\frac{2}{3}$π | D. | $\frac{1}{3}$π |
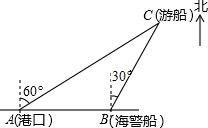 一艘观光游船从港口A以北偏东60°的方向出港观光,航行60海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东30°方向,马上以40海里每小时的速度前往救援,海警船到达事故船C处所需的时间大约为$\frac{\sqrt{3}}{2}$小时(用根号表示).
一艘观光游船从港口A以北偏东60°的方向出港观光,航行60海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东30°方向,马上以40海里每小时的速度前往救援,海警船到达事故船C处所需的时间大约为$\frac{\sqrt{3}}{2}$小时(用根号表示).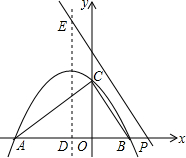 如图,二次函数y=ax2+bx+3的图象抛物线与其对称轴交于点(-1,m),与x轴交于点A和点B(2,0),与y轴交于点C,其对称轴与x轴交于点D.
如图,二次函数y=ax2+bx+3的图象抛物线与其对称轴交于点(-1,m),与x轴交于点A和点B(2,0),与y轴交于点C,其对称轴与x轴交于点D.