题目内容
20.若实数x,y满足|x-4|+$\sqrt{y-8}$=0,则以x,y的值为两边长的等腰三角形的周长是( )| A. | 12 | B. | 16 | C. | 16或20 | D. | 20 |
分析 根据非负数的意义列出关于x、y的方程并求出x、y的值,再根据x是腰长和底边长两种情况讨论求解.
解答 解:根据题意得
x-4=0,解得x=4,
y-8=0,解得y=8,
(1)若4是腰长,则三角形的三边长为:4、4、8,不能组成三角形;
(2)若4是底边长,则三角形的三边长为:4、8、8,能组成三角形,周长为4+8+8=20.
故选:D.
点评 本题考查了等腰三角形的性质、非负数的性质及三角形三边关系;解题主要利用了非负数的性质,分情况讨论求解时要注意利用三角形的三边关系对三边能否组成三角形做出判断.根据题意列出方程是正确解答本题的关键.

练习册系列答案
相关题目
10.我国质检总局规定,针织内衣等直接接触皮肤的制品,每千克的衣物上甲醛含量应在0.000075千克以下.将0.000075用科学记数法表示正确的是( )
| A. | 7.5×105 | B. | 75×10-6 | C. | 0.75×10-4 | D. | 7.5×10-5 |
8.下列命题是假命题的是( )
| A. | 三角形的中线平分三角形的面积 | |
| B. | 三角形的角平分线交点到三角形各边距离相等 | |
| C. | 三角形的高线至少有两条在三角形内部 | |
| D. | 三角形外心是三边垂直平分线的交点 |
9.已知x2-2x-5=0,则2x2-4x的值为( )
| A. | -10 | B. | 10 | C. | -2或10 | D. | 2或-10 |
 如图,AB∥CD,CP交AB于点O,AO=PO,∠C=50°,则∠A=25°.
如图,AB∥CD,CP交AB于点O,AO=PO,∠C=50°,则∠A=25°.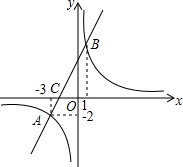 如图,一次函数y=kx+b图象与反比例函数y=$\frac{m}{x}$的图象交于点A、B,与x轴交于点C.
如图,一次函数y=kx+b图象与反比例函数y=$\frac{m}{x}$的图象交于点A、B,与x轴交于点C.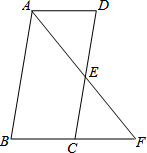 如图,在?ABCD中,点E是DC的中点,连接AE,并延长交BC的延长线于点F.
如图,在?ABCD中,点E是DC的中点,连接AE,并延长交BC的延长线于点F.