题目内容
20.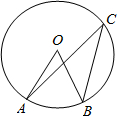 如图,点A、B、C都在⊙O上,⊙O的半径为2,∠ACB=30°,则$\widehat{AB}$的长是( )
如图,点A、B、C都在⊙O上,⊙O的半径为2,∠ACB=30°,则$\widehat{AB}$的长是( )| A. | 2π | B. | π | C. | $\frac{2}{3}$π | D. | $\frac{1}{3}$π |
分析 根据圆周角定理可得出∠AOB=60°,再根据弧长公式的计算即可.
解答 解:∵∠ACB=30°,
∴∠AOB=60°,
∵OA=2,
∴$\widehat{AB}$=$\frac{nπr}{180°}$=$\frac{60π•2}{180}$=$\frac{2}{3}$π,
故选:C.
点评 本题考查了弧长的计算以及圆周角定理,解题关键是掌握弧长公式l=$\frac{nπr}{180°}$.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
8. 某校学生来自甲、乙、丙三个地区,其人数比为2:3:5,如图所示的扇形统计图表上述分布情况.已知来自甲地区的为160人,则下列说法不正确的是( )
某校学生来自甲、乙、丙三个地区,其人数比为2:3:5,如图所示的扇形统计图表上述分布情况.已知来自甲地区的为160人,则下列说法不正确的是( )
 某校学生来自甲、乙、丙三个地区,其人数比为2:3:5,如图所示的扇形统计图表上述分布情况.已知来自甲地区的为160人,则下列说法不正确的是( )
某校学生来自甲、乙、丙三个地区,其人数比为2:3:5,如图所示的扇形统计图表上述分布情况.已知来自甲地区的为160人,则下列说法不正确的是( )| A. | 扇形甲的圆心角是72° | |
| B. | 学生的总人数是800人 | |
| C. | 丙地区的人数比乙地区的人数多160人 | |
| D. | 甲地区的人数比丙地区的人数少160人 |
15.我校举行了“建设宜居中山,关注环境保护”的知识竞赛,某班学生的成绩统计如下:
则该班学生成绩的众数和中位数分别是( )
| 成绩(分) | 60 | 70 | 80 | 90 | 100 |
| 人数 | 4 | 8 | 12 | 11 | 5 |
| A. | 70分,80分 | B. | 80分,80分 | C. | 90分,80分 | D. | 80分,90分 |
12.已知一个正多边形一个外角是72°,则这个正多边形是( )
| A. | 四边形 | B. | 五边形 | C. | 六边形 | D. | 七边形 |
10.下列命题错误的是( )
| A. | 已知菱形的两条对角线长分别是a、b,则这个菱形的面积为$\frac{1}{2}$ab | |
| B. | 在Rt△ABC中,若∠C=90°,∠A=30°,则AB=2CD | |
| C. | 在平面直角坐标系中,到x轴的距离为2,到y轴的距离为3的点的坐标是(3,2) | |
| D. | 在平面直角坐标系中,已知点P(2,-2),将线段OP绕着点O按顺时针方向旋转90°到OP′,则点P′的坐标是(-2,-2) |